题目内容
6．若关于x的不等式|x-1|+x≤a无解，则实数a的取值范围是（ ）| A． | （-∞，1） | B． | （∞，1] | C． | （1，+∞） | D． | [1，+∞） |
分析 通过去掉绝对值符号化简不等式的左侧为函数的表达式，通过函数的最值求出a的范围．
解答 解：令y=x+|x-1|=$\left\{\begin{array}{l}{2x-1，x≥1}\\{1，x＜1}\end{array}\right.$，
∴函数的最小值为1，
∴要使关于x的不等式x+|x-1|≤a无解，
实数a的取值范围为a＜1．
故选：A．
点评 本题考查绝对值不等式的解法，函数的最值的应用，基本知识的考查．
练习册系列答案
相关题目
10．已知$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，且|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|，则$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$上的投影为（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{2\sqrt{6}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
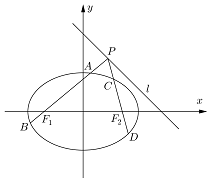已知椭圆$M：\frac{x^2}{2}+{y^2}=1$左、右焦点分别为F1、F2，点p为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点；
将全体正整数ai，j从左向右排成一个直角三角形数阵：