题目内容
1.若函数y=sin3x+acos3x的图象关于$x=-\frac{π}{9}$对称,则a=-$\frac{\sqrt{3}}{3}$.分析 利用三角恒等变换得出y=$\sqrt{{a}^{2}+1}$sin(3x+φ),根据对称轴得出φ的值,再利用sinφ=-$\frac{1}{2}$得出a的值.
解答 解:y=$\sqrt{{a}^{2}+1}$sin(3x+φ),其中,sinφ=$\frac{a}{\sqrt{{a}^{2}+1}}$,cosφ=$\frac{1}{\sqrt{{a}^{2}+1}}$,
∵函数图象关于x=-$\frac{π}{9}$对称,
∴-$\frac{π}{3}$+φ=$\frac{π}{2}$+kπ,即φ=$\frac{5π}{6}$+kπ,k∈Z.
∵cosφ=$\frac{1}{\sqrt{{a}^{2}+1}}$>0,
∴φ=-$\frac{π}{6}$+2kπ,∴sinφ=-$\frac{1}{2}$,
∴$\frac{a}{\sqrt{{a}^{2}+1}}$=-$\frac{1}{2}$,解得a=-$\frac{\sqrt{3}}{3}$.
故答案为:$-\frac{{\sqrt{3}}}{3}$.
点评 本题考查了三角恒等变换,正弦函数的图象与性质,属于中档题.

练习册系列答案
相关题目
12.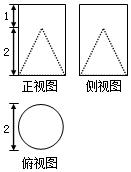 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )| A. | (7+$\sqrt{5}$)π | B. | (7+2$\sqrt{5}$)π | C. | (8+$\sqrt{5}$)π | D. | (8+2$\sqrt{5}$)π |
6.若关于x的不等式|x-1|+x≤a无解,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (∞,1] | C. | (1,+∞) | D. | [1,+∞) |
13.若(ax+2)4展开式中含有x3项的系数为8则$\int_a^{e^2}{\frac{1}{x}dx=}$( )
| A. | .2 | B. | .$-\frac{1}{e^2}-1$ | C. | .$-\frac{1}{e^2}+1$ | D. | 2-e |
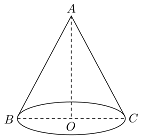 已知圆锥的侧面展开图是一个半圆;
已知圆锥的侧面展开图是一个半圆;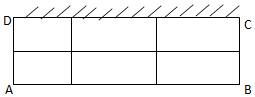 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?