函数y=tanx在点$({\frac{π}{3}.\sqrt{3}})$处的切线斜率为4．题目和参考答案——青夏教育精英家教网—

题目内容

18．函数y=tanx在点$（{\frac{π}{3}，\sqrt{3}}）$处的切线斜率为4．

分析求导数，可得曲线y=tanx在点（$\frac{π}{3}$，$\sqrt{3}$）处的切线的斜率．

解答解：y=$\frac{sinx}{cosx}$，y′=$\frac{1}{{cos}^{2}x}$，
x=$\frac{π}{3}$，y′=4，
∴曲线y=tanx在点（$\frac{π}{3}$，$\sqrt{3}$）处的切线的斜率为4，
故答案为：4．

点评本题考查导数的几何意义，考查学生的计算能力，比较基础．

练习册系列答案

$\frac{4\sqrt{5}}{3}$

B．

4$\sqrt{5}$

C．

$\frac{8\sqrt{5}}{3}$

D．

8$\sqrt{5}$

9．若长度为x²+4，4x，x²+6的三条线段可以构成一个锐角三角形，则x取值范围是x$＞\frac{\sqrt{15}}{3}$．

6．若关于x的不等式|x-1|+x≤a无解，则实数a的取值范围是（　　）

13．若（ax+2）⁴展开式中含有x³项的系数为8则$\int_a^{e^2}{\frac{1}{x}dx=}$（　　）

3．数列{a_n}中，a₁=1，a_n+1=2a_n+2，则a₇的值为（　　）

10．已知数列{a_n}为等差数列，且a₁=1，a₅=5，等比数列{b_n}的前n项和${S_n}=2-\frac{1}{{{2^{n-1}}}}，（n∈{N^*}）$．
（1）求数列{a_n}，{b_n}的通项公式；
（2）若c_n=a_nb_n（n=1，2，3，…），T_n为数列{c_n}的前n项和，求T_n．

7．

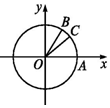在如图所示的直角坐标系xOy中，点A，B是单位圆上的点，且A（1，0），∠AOB=$\frac{π}{3}$．现有一动点C在单位圆的劣弧$\widehat{AB}$上运动，设∠AOC=α．
（1）若tanα=$\frac{1}{3}$，求$\overrightarrow{OB}$•$\overrightarrow{OC}$的值；
（2）若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，其中x，y∈R，求x+y的最大值．

8．已知向量$\overrightarrow a=（1，\sqrt{3}）$，$\overrightarrow b=（cosx，sinx）$，函数$f（x）=\overrightarrow a•\overrightarrow b-1$．
（1）若f（x）=0，求x的集合；
（2）若$x∈[0，\frac{π}{2}]$，求f（x）的单调区间及最值．

试题分类