题目内容

14．函数f（x）=x2-4x+5在区间[-1，m]上的最大值为10，最小值为1，则实数m的取值范围是（　　）
A．[2，+∞）B．[2，4]C．[-1，5]D．[2，5]

分析 由函数的解析式可得函数f（x）=x2-4x+5=（x-2）2+1的对称轴为x=2，此时，函数取得最小值为1，当x=-1或x=5时，函数值等于10，结合题意求得m的范围．

解答 解：∵函数f（x）=x2-4x+5=（x-2）2+1的对称轴为x=2，此时，函数取得最小值为1，
当x=-1或x=5时，函数值等于10．
且f（x）=x2-4x+5在区间[-1，m]上的最大值为10，最小值为1，
∴实数m的取值范围是[2，5]，
故选：D．

点评 本题主要考查二次函数的性质应用，注意函数的开口方向以及对称轴，属于中档题．

练习册系列答案
相关题目
4．已知复数z与（z+2）2+5均为纯虚数，则复数z=±3i．
5．函数$f（x）=ln（{x-\frac{1}{x}}）$的图象是（　　）
A．B．C．D．
2．如图，在平行四边形ABCD中，$\overrightarrow{AB}+\overrightarrow{AD}$=（　　）
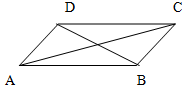
A．$\overrightarrow{AC}$B．$\overrightarrow{CA}$C．$\overrightarrow{BD}$D．$\overrightarrow{DB}$
9．已知函数f（x）=x2+|x|-|x-5|+2．
（1）求不等式f（x）＜0的解集；
（2）若关于x的不等式|f（x）|≤m的整数解仅有11个，求m的取值范围．
19．已知函数$f（x）=ax+\frac{b}{x}$（其中a，b为常数）的图象经过（1，2），$（{2\;，\;\;\frac{5}{2}}）$两点．
（1）求函数f（x）的解析式；
（2）证明函数f（x）在（1，+∞）是增函数；
（3）若不等式$\frac{{{{25}^m}}}{3}-{5^m}≥f（x）$对任意$x∈[{\frac{1}{2}\;，\;\;3}]$恒成立，求实数m的取值范围．
6．已知函数f（x）=x2e2x+m|x|ex+1（m∈R）有四个零点，则m的取值范围为（　　）
A．（-∞，-e-$\frac{1}{e}$）B．（-∞，e+$\frac{1}{e}$）C．（-e-$\frac{1}{e}$，-2）D．（-∞，-$\frac{1}{e}$）
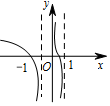
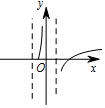
3．函数y=x5-xex的图象大致是（　　）
A．B．C．D．
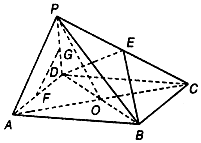4．如图，在四棱锥P-ABCD中，四边形ABCD为平行四边形，AC、BD相交于点O，点E、F、G分别为PC、AD、PD的中点，OP=OA，PA⊥PD．
求证：（1）FG∥平面BDE；
（2）平面BDE⊥平面PCD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网