题目内容
6.已知函数f(x)=x2e2x+m|x|ex+1(m∈R)有四个零点,则m的取值范围为( )| A. | (-∞,-e-$\frac{1}{e}$) | B. | (-∞,e+$\frac{1}{e}$) | C. | (-e-$\frac{1}{e}$,-2) | D. | (-∞,-$\frac{1}{e}$) |
分析 令y=xex,则y'=(1+x)ex,求出极值点,判断函数的单调性,作出y=xex图象,利用图象变换得f(x)=|xex|图象,令f(x)=t,则关于t方程h(t)=t2+mt+1=0两根分别在$(0,\frac{1}{e}),(\frac{1}{e},+∞)$,满足g(x)=-1的x有4个,列出不等式求解即可.
解答 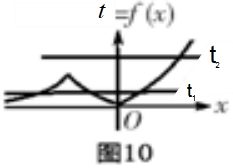 解:令y=xex,则y'=(1+x)ex,由y'=0,得x=-1,
解:令y=xex,则y'=(1+x)ex,由y'=0,得x=-1,
当x∈(-∞,-1)时,y'<0,函数y单调递减,
当x∈(-1,+∞)时,y'>0,函
数y单调递增.作出y=xex图象,
利用图象变换得f(x)=|xex|图象(如图10),
令f(x)=t,则关于t方程h(t)=t2+mt+1=0两根分别在$(0,\frac{1}{e}),(\frac{1}{e},+∞)$时(如图11),
满足g(x)=-1的x有4个,由$h(\frac{1}{e})=\frac{1}{{e}^{2}}+\frac{1}{e}m+1<0$,
解得m<-e-$\frac{1}{e}$. 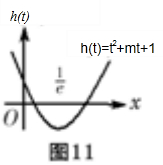
故选:A.
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,函数的图象的变换,函数零点个数,考查函数与方程的综合应用,数形结合思想以及转化思想的应用.

练习册系列答案
相关题目
16.已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{k}$=1的两个焦点分别为F1,F2,其一条渐近线的方程为y=x,若点P(m,1)在双曲线上,则$\overrightarrow{PF}$$•\overrightarrow{P{F}_{2}}$的值是( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
14.函数f(x)=x2-4x+5在区间[-1,m]上的最大值为10,最小值为1,则实数m的取值范围是( )
| A. | [2,+∞) | B. | [2,4] | C. | [-1,5] | D. | [2,5] |
11.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有xf′(x)>x2+3f(x),则不等式8f(x+2014)+(x+2014)3f(-2)>0的解集为( )
| A. | (-∞,-2016) | B. | (-2018,-2016) | C. | (-2018,0) | D. | (-∞,-2018) |
15.设复数z满足(1-i)z=3+i,则z=( )
| A. | 1+2i | B. | 2+2i | C. | 2-i | D. | 1+i |
16.已知圆C:(x-$\sqrt{3}$)2+(y-1)2=1和两点A(-t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )
| A. | ($\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$) | B. | ($\frac{3\sqrt{2}}{2}$,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$) | D. | ($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$) |
 如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC=30°,PA=AB=4.
如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC=30°,PA=AB=4.