题目内容
4.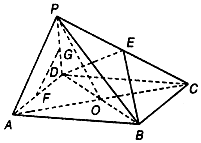 如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC、BD相交于点O,点E、F、G分别为PC、AD、PD的中点,OP=OA,PA⊥PD.
如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC、BD相交于点O,点E、F、G分别为PC、AD、PD的中点,OP=OA,PA⊥PD.求证:(1)FG∥平面BDE;
(2)平面BDE⊥平面PCD.
分析 (1)通过线线平行去证明线面平行即可.只需证明FG||OE即可.
(2)面面垂直转化为线面垂直,只需证明OE垂直平面PCD即可
解答 解:(1)∵点E、F、G分别为PC、AD、PD的中点,四边形ABCD为平行四边形
∴GE||DC,且GE=$\frac{1}{2}$DC,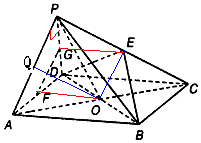
OF||DC,且OF=$\frac{1}{2}$DC,
∴OF||GE且GE=OF
故得四边形OFGE为平行四边形.
∴FG∥EO,
EO∈平面BDE,FG∉平面BDE,
∴FG∥平面BDE;
(2)由题意,FG∥AP,PA⊥PD,
∴FG⊥PD,
∵FG∥EO,
∴EO⊥PD,
又OP=OA,取AP的中点Q,连接OQ,
则OQ⊥AP,OQ∥PC,
∴PC⊥AP,
AP∥FG∥EO,
∴EO⊥PC,
∵$\left\{\begin{array}{l}{PC∈平面PCD}\\{PD∈平面PCD}\\{PD∩PC=P}\end{array}\right.$,
∴EO⊥平面PCD.
∵EO∈平面PCD,
故而平面BDE⊥平面PCD.
点评 本题考查了线面、面面平行,线面、面面垂直等简单的立体几何知识,考查学生对书本知识的掌握情况以及空间想象、推理能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.函数f(x)=x2-4x+5在区间[-1,m]上的最大值为10,最小值为1,则实数m的取值范围是( )
| A. | [2,+∞) | B. | [2,4] | C. | [-1,5] | D. | [2,5] |
15.设复数z满足(1-i)z=3+i,则z=( )
| A. | 1+2i | B. | 2+2i | C. | 2-i | D. | 1+i |
19.若函数$y=sin({2x+φ})({0<φ<\frac{π}{2}})$的图象的对称中心在区间$({\frac{π}{6},\frac{π}{3}})$内有且只有一个,则φ的值可以是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
9.已知函数f(x)=sin(ωx+φ)(0<ω<1,|φ|<π).若对任意x∈R,f(1)≤f(x)≤f(6),则( )
| A. | f(2014)-f(2017)<0 | B. | f(2014)-f(2017)=0 | C. | f(2014)+f(2017)<0 | D. | f(2014)+f(2017)=0 |
16.已知圆C:(x-$\sqrt{3}$)2+(y-1)2=1和两点A(-t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )
| A. | ($\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$) | B. | ($\frac{3\sqrt{2}}{2}$,$\frac{3}{2}$) | C. | ($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$) | D. | ($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$) |
13.已知全集U={-2,0,1,2},集合A={x|x2-2x=0},则∁UA=( )
| A. | {-2,1} | B. | {-2,0,2} | C. | {0,2} | D. | {0,1} |
14.甲、乙、丙 3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数是( )
| A. | 210 | B. | 84 | C. | 343 | D. | 336 |