题目内容
5.函数$f(x)=ln({x-\frac{1}{x}})$的图象是( )| A. | 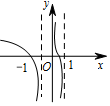 | B. | 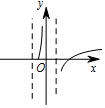 | C. |  | D. |  |
分析 求出函数的定义域,排除选项,利用函数的单调性判断求解即可.
解答 解:函数$f(x)=ln({x-\frac{1}{x}})$,可得x$-\frac{1}{x}>0$,可得x>1或-1<x<0,
排除选项A,D;
当x>1时,y=x-$\frac{1}{x}$是增函数,由复合函数的单调性可知,函数$f(x)=ln({x-\frac{1}{x}})$,x>1是增函数,
排除C,
故选:B.
点评 本题考查函数的图象的判断,函数的定义域以及函数的单调性的常用判断方法.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
5.已知集合M={x|(x-3)(x+1)≤0},N={x|-2≤x≤2},则M∩N=( )
| A. | [-1,2] | B. | [-2,-1] | C. | [-1,1] | D. | [1,2] |
16.已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{k}$=1的两个焦点分别为F1,F2,其一条渐近线的方程为y=x,若点P(m,1)在双曲线上,则$\overrightarrow{PF}$$•\overrightarrow{P{F}_{2}}$的值是( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
10.下列四个命题中真命题是( )
| A. | 同垂直于一直线的两条直线互相平行 | |
| B. | 底面各边相等,侧面都是矩形的四棱柱是正四棱柱 | |
| C. | 过空间任一点与两条异面直线都垂直的直线有且只有一条 | |
| D. | 过球面上任意两点的大圆有且只有一个 |
14.函数f(x)=x2-4x+5在区间[-1,m]上的最大值为10,最小值为1,则实数m的取值范围是( )
| A. | [2,+∞) | B. | [2,4] | C. | [-1,5] | D. | [2,5] |
15.设复数z满足(1-i)z=3+i,则z=( )
| A. | 1+2i | B. | 2+2i | C. | 2-i | D. | 1+i |
 如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC=30°,PA=AB=4.
如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC=30°,PA=AB=4.