题目内容
9.f(x)为R上奇函数,当x≥0时,f(x)=x+1,则当x<0时,f(x)=x-1.分析 利用f(x)为R上奇函数,f(-x)=-f(x),当x≥0时,f(x)=x+1,可求x<0的解析式.
解答 解:由题意,函数f(x)为R上奇函数,f(-x)=-f(x),
当x≥0时,f(x)=x+1,
当x<0时,则-x>0,那么f(-x)=-x+1.
∵f(-x)=-f(x),
∴f(x)=x-1,
故答案为:x-1,
点评 本题考查了函数的性质的运用,利用了函数是奇函数这性质.比较基础.

练习册系列答案
相关题目
14.在△ABC中,b=35,c=20,C=30°,则此三角形解的情况是( )
| A. | 两解 | B. | 一解 | C. | 一解或两解 | D. | 无解 |
1.已知数列{an}满足${a_1}=2,{a_{n+1}}=\frac{{{a_n}-1}}{{{a_n}+1}}(n∈N*)$,则该数列的前2017项的乘积a1a2a3…a2017=( )
| A. | 2 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -2 |
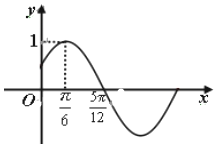 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.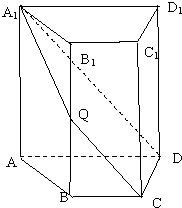 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.