题目内容
已知锐角△ABC,函数f(x)=(sinA-cosB)x2-(sinB-cosA)x+sinC,x∈R,如果对于任意的实数x都有f(1-x)=f(x).有下列结论:①f(0)>f(
);②△ABC为等边三角形;③f(x)有最大值;④f(x)的最小值的取值范围是(-
,1).上述结论中,正确结论的序号为( )
| 1 |
| 2 |
| 1 |
| 4 |
| A、①③ | B、①④ | C、②③ | D、②④ |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:由题意得二次函数的对称轴为x=
,又△ABC为锐角三角形,并且A+B>
,有sinA-cosB>0,得对称轴为:x=0.5,可得①正确,③错误;排除A,C选项.由二次函数对称轴x=
=
,整理得A=B或A+B=
;故②错误;排除D选项即可得解.
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| sinB-cosA |
| 2(sinA-cosB) |
| π |
| 2 |
解答:
解:由题意对于任意的实数x都有f(1-x)=f(x),
则二次函数函数的对称轴为x=
,
又△ABC为锐角三角形,并且A+B>
,即A>
-B,
所以sinA>sin(
-B)=cosB,
所以sinA-cosB>0,
所以二次函数开口向上,对称轴为:x=0.5,所以①正确,③错误;排除A,C选项.
由二次函数对称轴x=
=
,
所以sinB-cosA=sinA-cosB,
所以sinB+cosB=sinA+cosA,平方整理得sin2B=sin2A,所以A=B或A+B=
;故②错误;排除D选项.
故选:B.
则二次函数函数的对称轴为x=
| 1 |
| 2 |
又△ABC为锐角三角形,并且A+B>
| π |
| 2 |
| π |
| 2 |
所以sinA>sin(
| π |
| 2 |
所以sinA-cosB>0,
所以二次函数开口向上,对称轴为:x=0.5,所以①正确,③错误;排除A,C选项.
由二次函数对称轴x=
| 1 |
| 2 |
| sinB-cosA |
| 2(sinA-cosB) |
所以sinB-cosA=sinA-cosB,
所以sinB+cosB=sinA+cosA,平方整理得sin2B=sin2A,所以A=B或A+B=
| π |
| 2 |
故选:B.
点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,考查了二次函数的图象和性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
投掷两颗质地均匀的骰子,则向上的点数之积为6的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
平面内过点A(-2,0),且与直线x=2相切的动圆圆心的轨迹方程是( )
| A、y2=-2x |
| B、y2=-4x |
| C、y2=-8x |
| D、y2=-16x |
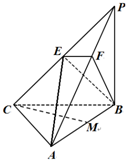 在三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.
在三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.