题目内容
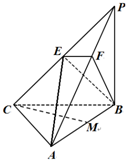 在三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.
在三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.(Ⅰ)求证:AC⊥平面PBC;
(Ⅱ)求证:CM∥平面BEF;
(Ⅲ)若PB=BC=CA=2,求三棱锥E-ABC的体积.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)由PB⊥底面ABC,可证AC⊥PB,由∠BCA=90°,可得AC⊥CB.又PB∩CB=B,即可证明AC⊥平面PBC.
(Ⅱ)取AF的中点G,连结CG,GM.可得EF∥CG.又CG?平面BEF,有EF?平面BEF,有CG∥平面BEF,同理证明GM∥平面BEF,有平面CMG∥平面BEF,即可证明CM∥平面BEF.
(Ⅲ)取BC中点D,连结ED,可得ED∥PB,由PB⊥底面ABC,故ED⊥底面ABC,由PB=BC=CA=2,即可求得三棱锥E-ABC的体积.
(Ⅱ)取AF的中点G,连结CG,GM.可得EF∥CG.又CG?平面BEF,有EF?平面BEF,有CG∥平面BEF,同理证明GM∥平面BEF,有平面CMG∥平面BEF,即可证明CM∥平面BEF.
(Ⅲ)取BC中点D,连结ED,可得ED∥PB,由PB⊥底面ABC,故ED⊥底面ABC,由PB=BC=CA=2,即可求得三棱锥E-ABC的体积.
解答:
 (共14分)
(共14分)
证明:(Ⅰ)因为PB⊥底面ABC,且AC?底面ABC,
所以AC⊥PB.
由∠BCA=90°,可得AC⊥CB.
又PB∩CB=B,
所以AC⊥平面PBC. …(5分)
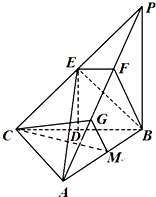
(Ⅱ)取AF的中点G,连结CG,GM.
因为AF=2FP,G为AF中点,所以F为PG中点.
在△PCG中,E,F分别为PC,PG中点,
所以EF∥CG.又CG?平面BEF,EF?平面BEF,
所以CG∥平面BEF.
同理可证GM∥平面BEF.
又CG∩GM=G,
所以平面CMG∥平面BEF.
又CM?平面CMG,
所以CM∥平面BEF.…(11分)
(Ⅲ)取BC中点D,连结ED.
在△PBC中,E,D分别为中点,所以ED∥PB.
因为PB⊥底面ABC,所以ED⊥底面ABC.
由PB=BC=CA=2,可得V=
S△ABC•ED=
×
×2×2×1=
. …(14分)
 (共14分)
(共14分)证明:(Ⅰ)因为PB⊥底面ABC,且AC?底面ABC,
所以AC⊥PB.
由∠BCA=90°,可得AC⊥CB.
又PB∩CB=B,
所以AC⊥平面PBC. …(5分)
(Ⅱ)取AF的中点G,连结CG,GM.
因为AF=2FP,G为AF中点,所以F为PG中点.
在△PCG中,E,F分别为PC,PG中点,
所以EF∥CG.又CG?平面BEF,EF?平面BEF,
所以CG∥平面BEF.
同理可证GM∥平面BEF.
又CG∩GM=G,
所以平面CMG∥平面BEF.
又CM?平面CMG,
所以CM∥平面BEF.…(11分)
(Ⅲ)取BC中点D,连结ED.
在△PBC中,E,D分别为中点,所以ED∥PB.
因为PB⊥底面ABC,所以ED⊥底面ABC.
由PB=BC=CA=2,可得V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,三棱锥体积公式的应用,正确做出相应的辅助线是解题的关键,考查了转化思想,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
若直线l的方向向量为
=(1,-1,2),平面α的法向量为
=(-2,2,-4),则( )
| a |
| u |
| A、l∥α | B、l⊥α |
| C、l?α | D、l与α斜交 |