题目内容
设b>0,a≠0,若函数f(x)=
的定义域与值域相等,则a= .
| ax2+bx |
考点:函数的值域,函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数的定义域与值域相同,故可以求出参数表示的函数的定义域与值域,由两者相同,
故比较二区间的端点得出参数满足的方程解方程求参数即可.
故比较二区间的端点得出参数满足的方程解方程求参数即可.
解答:
解:若a>0,对于正数b,f(x)的定义域为D=(-∞,-
)∪(0,+∞),
但f(x)的值域A⊆[0,+∞),故D≠A,不合要求.
若a<0,对于正数b,f(x)的定义域为 D=[0,-
].
由于此时f(x)max=f(-
)]=f(-
)=
,
故函数的值域 A=[0,
].
由题意,有-
=
,由于b>0,所以a=-4.
若a=0,则对于每个正数b,f(x)=
的定义域和值域都是[0,+∞)
故a=0满足条件.
故答案为:-4或0.
| b |
| a |
但f(x)的值域A⊆[0,+∞),故D≠A,不合要求.
若a<0,对于正数b,f(x)的定义域为 D=[0,-
| b |
| a |
由于此时f(x)max=f(-
| b |
| a |
| b |
| 2a |
| b | ||
2
|
故函数的值域 A=[0,
| b | ||
2
|
由题意,有-
| b |
| a |
| b | ||
2
|
若a=0,则对于每个正数b,f(x)=
| bx |
故a=0满足条件.
故答案为:-4或0.
点评:本题考查的知识点是函数的定义域及其求法,函数的值域,二次函数的图象和性质,其中熟练掌握一次函数和二次函数的图象和性质是解答本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
非零向量
,
满足2
•
=
2
2,|
|+|
|=2,则
,
的夹角θ的最小值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(-3,4),
=(1,m),若
•(
-
)=0,则m=( )
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
| C、7 | ||
| D、-7 |
设数列{an}的前n项和为Sn,且a1=1,{Sn+nan}为常数列,则an=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
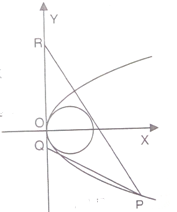 如图,已知抛物线C:y2=2px(p>0)上的点(
如图,已知抛物线C:y2=2px(p>0)上的点(