题目内容
函数f(x)=
的定义域是 .
| ||
| x |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由根式内部的代数式大于等于0且分式的分母不等于0联立不等式组求解x的取值集合得答案.
解答:
解:由
,得x≥-1且x≠0.
∴函数f(x)=
的定义域为:[-1,0)∪(0,+∞);
故答案为:[-1,0)∪(0,+∞).
|
∴函数f(x)=
| ||
| x |
故答案为:[-1,0)∪(0,+∞).
点评:本题考查了函数的定义域及其求法,是基础的会考题型.

练习册系列答案
相关题目
已知
,
,
表示共面的三个单位向量,
⊥
,那么(
+
)•(
+
)的取值范围是( )
| i |
| j |
| k |
| i |
| j |
| i |
| k |
| j |
| k |
| A、[-3,3] | ||||
| B、[-2,2] | ||||
C、[
| ||||
D、[1-
|
对于定义在实数集R上的函数f(x),若f(x)与f(x+1)都是偶函数,则( )
| A、f(x)是奇函数 |
| B、f(x-1)是奇函数 |
| C、f(x+2)是偶函数 |
| D、f(x+3)是奇函数 |
已知直线a,b,平面α,β,且a⊥α,b?β,则“a⊥b”是“α∥β”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
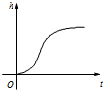
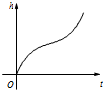
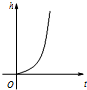
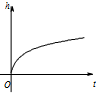
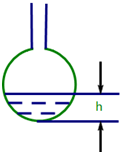 匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )
匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )