题目内容

10．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案，则第2016个图案中的白色地面砖有8066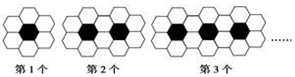

分析 通过观察前几个图形中正六边形地面砖的个数得，每一个图形中的正六边形地面砖个数都可以看成是一个等差数列的项，再利用等差数列的通项公式即可解决问题．

解答 解：第1个图案中有白色地面砖6块；第2个图案中有白色地面砖10块；第3个图案中有白色地面砖14块；…
设第n个图案中有白色地面砖n块，用数列{an}表示，则a1=6，a2=10，a3=14，可知a2-a1=a3-a2=4，…
可知数列{an}是以6为首项，4为公差的等差数列，∴an=6+4（n-1）=4n+2，
n=2016时，a2016=8066．
故答案为：8066．

点评 本题主要考查了归纳推理，以及观察能力和分析问题和解决的能力，属于基础题．

练习册系列答案
相关题目
20．关于x的方程cos2x+sinx+a=0在$x∈（{0，\frac{π}{2}}]$上有解，则a的取值范围是$[{-\frac{5}{4}，-1}]$．
1．下列求导错误的是（　　）
A．$（\frac{1}{x}）'=-\frac{1}{x^2}$B．$（\sqrt{x}）'=\frac{1}{{2\sqrt{x}}}$C．$（lnx）'=\frac{1}{x}$D．$（sin\frac{π}{3}）'=cos\frac{π}{3}$
18．在△ABC中，内角A、B、C所对的边为a、b、c，且$\sqrt{3}$asinC-c（2+cosA）=0．
（1）求角A的大小；
（2）若△ABC的最大边长为$\sqrt{7}$，且sinC=2sinB，求最小边长．
5．如图，梯形ABCD，|$\overrightarrow{DA}$|=2，∠CDA=$\frac{π}{3}$，$\overrightarrow{DA}$=2$\overrightarrow{CB}$，E为AB中点，$\overrightarrow{DP}$=λ$\overrightarrow{DC}$（0≤λ≤1）．
（Ⅰ）当λ=$\frac{1}{3}$，用向量$\overrightarrow{DA}$，$\overrightarrow{DC}$表示的向量$\overrightarrow{PE}$；
（Ⅱ）若|$\overrightarrow{DC}$|=t（t为大于零的常数），求|$\overrightarrow{PE}$|的最小值并指出相应的实数λ的值．
15．已知集合A={x|log2x＞2}，$B=\{x|{（\frac{1}{2}）^x}≥\frac{1}{16}\}$，则下列结论成立的是（　　）
A．A∩B=AB．（∁RA）∩B=AC．A∩（∁RB）=AD．（∁RA）∩（∁RB）=A
2．已知等比数列{an}的第2项、第5项分别为二项式（2x+1）5展开式的第5项、第2项的系数．
（1）求数列{an}的通项公式；
（2）记数列{an}的前n项和为Sn，若存在实数λ，使$\frac{λ}{{2{a_n}}}＞\frac{1}{a_n}-\frac{1}{S_n}$恒成立，求实数λ的取值范围．
19．函数$y={log_a}^{（4x-1）}$，（a＞0且a≠1）图象必过的定点是$（\frac{1}{2}，0）$．
20．设全集U=R，集合M={x|x＞1}，p={x|x2＞1}，则下列关系中正确的是（　　）
A．M=PB．P?MC．M?PD．（∁UM）∩P=∅

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网