题目内容
已知椭圆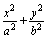 =1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足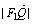 =2a,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
=2a,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足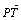 ·
·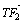 =0,|
=0,|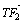 |≠0.
|≠0.
(1)设x为点P的横坐标,证明|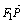 |=a+
|=a+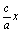 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2,若存在,求∠F1MF2的正切值;若不存在,请说明理由.
(1)证法一:设点P的坐标为(x,y).由P(x,y)在椭圆上,得
 2
2
由|x|≤a,知a+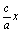 ≥-c+a>0,所以
≥-c+a>0,所以 =a+
=a+ x.
x.


(Ⅲ)解法一:C上存在点M(x0,y0)使S=b2的充要条件是



练习册系列答案
相关题目
 ,则λ=( ).
,则λ=( ). B.
B.
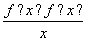 <0的解集为( ).
<0的解集为( ). A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)
A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)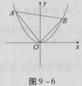
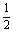 x严与抛物线y=
x严与抛物线y=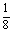 x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.
x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.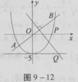
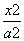 +
+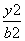 =1(a>b>0)的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若3
=1(a>b>0)的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若3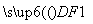 =
=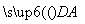 +2
+2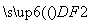 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )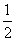 B.
B.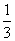
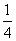 D.
D.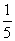
 中任取2个数字,从0、2、4、6、8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有__________个(用数字作答)。
中任取2个数字,从0、2、4、6、8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有__________个(用数字作答)。