题目内容
方程为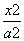 +
+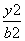 =1(a>b>0)的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若3
=1(a>b>0)的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若3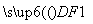 =
=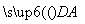 +2
+2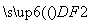 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A.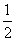 B.
B.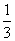
C.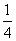 D.
D.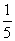
D

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
题目内容
方程为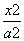 +
+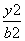 =1(a>b>0)的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若3
=1(a>b>0)的椭圆左顶点为A,左、右焦点分别为F1、F2,D是它短轴上的一个顶点,若3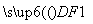 =
=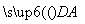 +2
+2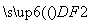 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A.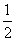 B.
B.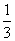
C.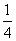 D.
D.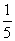
D

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案