题目内容
在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图所示)．
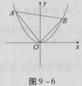
(1)求△AOB的重心C(即三角形三条中线的交点)的轨迹方程；
(Ⅱ)△AOB的面积是否存在最小值?若存在，请求出最小值；若不存在，请说明理由．
∵OA⊥OB．
(Ⅱ)S△AOB=
由(1)得S△AOB=
当且仅当x16=x26即x1=-x2=-1时，等号成立。
所以△AOB的面积存在最小值，最小值为1
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
的一条直线与函数f(x)＝
的图象交于P，Q两点，则线段PQ长的最小值是________．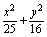
=1相交于A、B两点，l又与双曲线x2-y2=1相交于C、D两点，C、D三等分线段AB，求直线l的方程 
=x2，则点P的轨迹是 ( )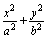
=1(a>b>0)的左、右焦点分别是F1(-c，0)、F2(c，0)，Q是椭圆外的动点，满足
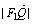=2a，点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足
·
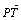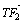=0，|
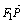|=a+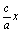
； 
＋
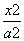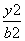＝1(a>b>0)的离心率为
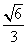，椭圆C上任意一点到椭圆C两个焦点的距离之和为6.
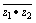是实数，则实数t= （ ）
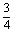B．
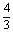C．-