题目内容
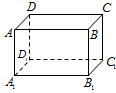如图，已知长方体AC1的长、宽、高分别为5、4、3，现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物，它爬行路线的路程最小值为考点：多面体和旋转体表面上的最短距离问题
专题：计算题,空间位置关系与距离
分析：求A点到C1的最短距离，由两点之间直线段最短，想到需要把长方体剪开再展开，把A到C1的最短距离转化为求三角形的边长问题，根据实际图形，应该有三种展法，展开后利用勾股定理求出每一种情况中AC1的长度，比较三个值的大小后即可得到结论．
解答：
解：把长方体含AC1的面作展开图，有三种情形如图所示：利用勾股定理可得AC1的长分别为
、
、
．
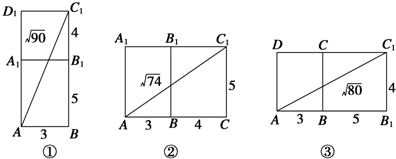
由此可见图②是最短线路，其路程的最小值为
．
故答案为：
．
| 90 |
| 74 |
| 80 |
由此可见图②是最短线路，其路程的最小值为
| 74 |
故答案为：
| 74 |
点评：本题考查了多面体和旋转体表面上的最短距离问题，考查了学生的空间想象能力和思维能力，考查了数学转化思想方法，解答的关键是想到对长方体的三种展法，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知x、y满足约束条件
，则z=2x+4y的最小值为（ ）
|
| A、-6 | B、5 | C、10 | D、-10 |
某网店经营的一红消费品的进价为每件12元，周销售量p（件）与销售价格x（元）的关系，如图中折线所示，每周各项开支合计为20元．下列命题正确的是（ ）
| A、垂直于同一直线的两条直线互相平行 |
| B、平行四边形在一个平面上的平行投影一定是平行四边形 |
| C、平面截正方体所得的截面图形可能是正六边形 |
| D、锐角三角形在一个平面上的平行投影不可能是钝角三角形 |
若函数f（x）=3x，它的反函数是g（x），a=g（3），b=g（4），c=g（π），则下面关系式中正确的是（ ）
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜c＜a |
| D、b＜a＜c |