题目内容
若不等式|x-1|+|x-2|≤a2+a+1的解集不为∅，则实数a的取值范围是 ．
考点：绝对值不等式的解法
专题：选作题,不等式
分析：令f（x）=|x-1|+|x-2|可求得f（x）min，依题意，a2+a+1≥f（x）min，解之即可．
解答：
解：令f（x）=|x-1|+|x-2|，由绝对值的几何意义：数轴上的点到1，3的结论之和，
可知函数f（x）的最小值为：1，
即f（x）min=1．
∵不等式|x-1|+|x-2|≤a2+a+1的解集不为∅，
∴a2+a+1≥f（x）min=1，
∴a2+a≥0．
解得：a≥0或a≤-1．
∴实数a的取值范围是（-∞，-1]∪[0，+∞）．
故答案为：（-∞，-1]∪[0，+∞）．
可知函数f（x）的最小值为：1，
即f（x）min=1．
∵不等式|x-1|+|x-2|≤a2+a+1的解集不为∅，
∴a2+a+1≥f（x）min=1，
∴a2+a≥0．
解得：a≥0或a≤-1．
∴实数a的取值范围是（-∞，-1]∪[0，+∞）．
故答案为：（-∞，-1]∪[0，+∞）．
点评：本题考查绝对值不等式，考查构造函数思想与方程思想，考查理解题意与推理运算的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
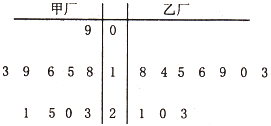为了解甲、乙两厂的产品质量，分别从两厂生产的产品中各随机抽取10件，测量产品中某种元素的含量（单位：毫克），其测量数据的茎叶图如图所示：规定：当产品中此种元素含量大于18毫克时，认定该产品为优等品．
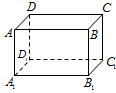如图，已知长方体AC1的长、宽、高分别为5、4、3，现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物，它爬行路线的路程最小值为已知函数f（x）=sin2x（x∈R），为了得到函数g（x）=sin（2x+
）的图象，只要将y=f（x）的图象（ ）
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|