题目内容
 某网店经营的一红消费品的进价为每件12元,周销售量p(件)与销售价格x(元)的关系,如图中折线所示,每周各项开支合计为20元.
某网店经营的一红消费品的进价为每件12元,周销售量p(件)与销售价格x(元)的关系,如图中折线所示,每周各项开支合计为20元.(1)写出周销售量p(件)与销售价格x(元)元的函数关系式;
(2)写出利润周利润y(元)与销售价格x(元)的函数关系式;
(3)当该消费品销售价格为多少元时,周利润最大?并求出最大周利润.
考点:函数模型的选择与应用,函数解析式的求解及常用方法,函数的图象
专题:应用题,函数的性质及应用
分析:(1)根据函数图象为分段函的图象,所以应求12≤x≤20,与20<x≤28两部分的解析式,由图象上的点分别代入p=ax+b,求出即可;
(2)利用周销售量与利润的积,可得利润周利润y(元)与销售价格x(元)的函数关系式;
(3)根据(2)分段求最值,即可得出结论.
(2)利用周销售量与利润的积,可得利润周利润y(元)与销售价格x(元)的函数关系式;
(3)根据(2)分段求最值,即可得出结论.
解答:
解:(1)由题设知,当12≤x≤20时,设p=ax+b,
则
,∴a=-2,b=50
∴p=-2x+50,
同理得,当20<x≤28时,p=-x+30,
所以p=
;
(2)当12≤x≤20时,y=(x-12)(-2x+50)=-2x2+74x-620;
当20<x≤28时,y=(x-12)(-x+30)-20=-x2+42x-380;
∴y=
;
(3)当12≤x≤20时,y=(x-12)(-2x+50)=-2x2+74x-620,
∴x=
时,y取得最大值
;
当20<x≤28时,y=(x-12)(-x+30)-20=-x2+42x-380,
∴x=21时,y取得最大值61;
∵
>61,
∴该消费品销售价格为
时,周利润最大,最大周利润为
.
则
|
∴p=-2x+50,
同理得,当20<x≤28时,p=-x+30,
所以p=
|
(2)当12≤x≤20时,y=(x-12)(-2x+50)=-2x2+74x-620;
当20<x≤28时,y=(x-12)(-x+30)-20=-x2+42x-380;
∴y=
|
(3)当12≤x≤20时,y=(x-12)(-2x+50)=-2x2+74x-620,
∴x=
| 37 |
| 2 |
| 129 |
| 2 |
当20<x≤28时,y=(x-12)(-x+30)-20=-x2+42x-380,
∴x=21时,y取得最大值61;
∵
| 129 |
| 2 |
∴该消费品销售价格为
| 37 |
| 2 |
| 129 |
| 2 |
点评:本题是一道综合题,难度较大.重点考查了一次函数图象和实际应用相结合的问题,能够从图象上准确地获取信息,本题中p与x的关系是分段的,要注意对应,这是做本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
一只蜜蜂在一个棱长为5的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于2,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
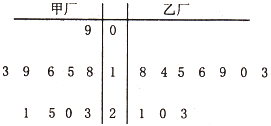 为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如图所示:规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品.
为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如图所示:规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品.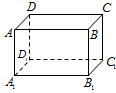 如图,已知长方体AC1的长、宽、高分别为5、4、3,现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物,它爬行路线的路程最小值为
如图,已知长方体AC1的长、宽、高分别为5、4、3,现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物,它爬行路线的路程最小值为