题目内容
已知x、y满足约束条件
,则z=2x+4y的最小值为( )
|
| A、-6 | B、5 | C、10 | D、-10 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
由z=2x+4y得y=-
x+
,
平移直线y=-
x+
,由图象可知当直线y=-
x+
经过点A时,
直线y=-
x+
的截距最小,此时z最小,
由
,解得
,即A(3,-3),
此时z=2×3+4×(-3)=-6,
故选:A

由z=2x+4y得y=-
| 1 |
| 2 |
| z |
| 4 |
平移直线y=-
| 1 |
| 2 |
| z |
| 4 |
| 1 |
| 2 |
| z |
| 4 |
直线y=-
| 1 |
| 2 |
| z |
| 4 |
由
|
|
此时z=2×3+4×(-3)=-6,
故选:A
点评:本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知定义在R上的奇函数f(x)满足f(2+x)=f(-x),当0≤x≤1时,f(x)=x2,则f(2015)=( )
| A、-1 |
| B、1 |
| C、0 |
| D、20152 |
一只蜜蜂在一个棱长为5的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于2,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图是一个算法流程图,则输出的x的值是
如图是一个算法流程图,则输出的x的值是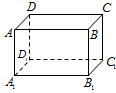 如图,已知长方体AC1的长、宽、高分别为5、4、3,现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物,它爬行路线的路程最小值为
如图,已知长方体AC1的长、宽、高分别为5、4、3,现有一甲壳虫从A点出发沿长方体表面爬到C1处获取食物,它爬行路线的路程最小值为