题目内容
11.若存在实数k和b,使得函数f(x)和g(x)对定义域内的任意x均满足:[f(x)-(kx+b)][g(x)-(kx+b)]≤0,且存在x1使得f(x1)-(kx1+b)=0,存在x2使得g(x2)-(kx2+b)=0,则称直线l:y=kx+b为函数f(x)和g(x)的“分界线”.在下列说法中正确的是( )| A. | 任意两个一次函数最多存在一条“分界线” | |
| B. | “分界线”存在的两个函数的图象最多只有两个交点 | |
| C. | f(x)=x2-2x与g(x)=-x2+4的“分界线”是y=-x+2 | |
| D. | f(x)=x2与g(x)=-(x-1)2的“分界线”是y=0或$y=x-\frac{1}{2}$ |
分析 由[f(x)-(kx+b)][g(x)-(kx+b)]≤0,可得f(x)和g(x)在直线y=kx+b的两侧,同时f(x)和g(x)都和直线y=kx+b相交,利用数形结合进行求解判断即可.
解答 解:由[f(x)-(kx+b)][g(x)-(kx+b)]≤0,可得f(x)和g(x)在直线y=kx+b的两侧,
由f(x1)-(kx1+b)=0和g(x2)-(kx2+b)=0得f(x)和g(x)都和直线y=kx+b相交,
A.任意两个函数相交时,过交点的直线有很多条,
故任意两个一次函数存在无数条“分界线”如图:故A错误,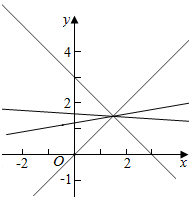
B.当f(x)=x(x-1)(x+1)+1,g(x)=-x(x-1)(x+1)+1,满足y=1是f(x)和g(x)的分界线,但此时f(x)与g(x)有3个交点,故B错误,
C.由x2-2x=-x2+4得x2-x-2=0,得x=2或x=-1,此时A(-1,3),B(2,0),过A,B的直线为y=-x+2,
则f(x)=x2-2x与g(x)=-x2+4的“分界线”是y=-x+2,故C正确,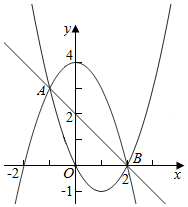
D.作出f(x),g(x)和y=0或$y=x-\frac{1}{2}$的图象,由图象知$y=x-\frac{1}{2}$与f(x)和g(x)没有交点,不满足条件f(x1)-(kx1+b)=0和g(x2)-(kx2+b)=0,.
故D错误,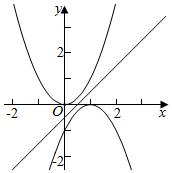
故选:C
点评 本题主要考查命题的真假判断,利用条件得到“分界线”的定义,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.集合A={x||x|≤4,x∈R},B={x||x-3|<a,x∈R},若A?B,那么a的取值范围是( )
| A. | 0≤a≤1 | B. | a≤1 | C. | a<1 | D. | 0<a<1 |
16.若函数f(x)=2x-3,则f-1(5)=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
3.已知△ABC中,$AB=\sqrt{3},AC=1$,且B=30°,则角C的大小为( )
| A. | 60°或120° | B. | 120° | C. | 60° | D. | 30° |
20.在下列各组函数中,两个函数相等的是( )
| A. | f(x)=$\root{3}{x^3}$与g(x)=$\root{4}{x^4}$ | |
| B. | f(x)=$\sqrt{{x^2}-1}$与g(x)=$\sqrt{x-1}•\sqrt{x+1}$ | |
| C. | f(x)=2x,x∈{0,1,2,3}与g(x)=$\frac{x^3}{6}+\frac{5}{6}x+1,x∈\left\{{0,1,2,3}\right\}$ | |
| D. | f(x)=|x|与g(x)=$\left\{\begin{array}{l}x,x≥0\\-x,x<0\end{array}$ |
1.在直角坐标系xOy中,已知点A(0,1),点B(-3,4),若点C在∠AOB的平分线上,则向量$\overrightarrow{OC}$可以等于( )
| A. | (-2,3) | B. | (-2,4) | C. | (-1,4) | D. | (-1,3) |