题目内容
2.已知函数f(x)=$|\begin{array}{l}{2sinx}&{m}\\{cos2x}&{cosx}\end{array}|$的图象关于直线x=$\frac{π}{8}$对称,则f(x)的单调递增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.分析 利用矩阵运算及正弦函数的图象的对称性求得m的值,再利用两角和差的正弦公式、正弦函数的单调性求得f(x)的单调递增区间.
解答 解:∵函数f(x)=$|\begin{array}{l}{2sinx}&{m}\\{cos2x}&{cosx}\end{array}|$=2sinxcosx-mcos2x=sin2x-mcos2x的图象关于直线x=$\frac{π}{8}$对称,
∴f(0)=f($\frac{π}{4}$),即-m=1,即m=-1.
则f(x)=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,
求得 kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$(k∈Z),故函数f(x)的单调递增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z,
故答案为:[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
点评 本题主要考查矩阵、两角和差的正弦公式、正弦函数的单调性以及图象的对称性,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
11.若存在实数k和b,使得函数f(x)和g(x)对定义域内的任意x均满足:[f(x)-(kx+b)][g(x)-(kx+b)]≤0,且存在x1使得f(x1)-(kx1+b)=0,存在x2使得g(x2)-(kx2+b)=0,则称直线l:y=kx+b为函数f(x)和g(x)的“分界线”.在下列说法中正确的是( )
| A. | 任意两个一次函数最多存在一条“分界线” | |
| B. | “分界线”存在的两个函数的图象最多只有两个交点 | |
| C. | f(x)=x2-2x与g(x)=-x2+4的“分界线”是y=-x+2 | |
| D. | f(x)=x2与g(x)=-(x-1)2的“分界线”是y=0或$y=x-\frac{1}{2}$ |
8.一个三位自然数百位、十位、个位上的数字依次为a,b,c,当且仅当其中有两个数字的和等于第三个数字时称为“有缘数”(如213,341等).若a,b,c∈{1,2,3,4},且a,b,c互不相同,任取一个三位自然数,则它是“有缘数”的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
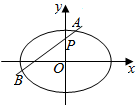 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.