题目内容
5.分析下列四个命题:①若实数a,b,c满足a+b+c=3,则a,b,c中至少有一个不小于1;
②若z为复数,且|z|=1,则|z-i|的最大值等于2;
③任意x∈(0,+∞)都有x>sinx;
④若f(x)是奇函数,则∫${\;}_{-a}^{a}$f(x)dx=2∫${\;}_{0}^{a}$f(x)dx.
其中,正确命题的序号是①②③.(把你认为正确命题的序号都填上)
分析 ①可运用反证法,即可判断;
②运用|z-i|≤|z|+|-i|=2,即可得到最大值;
③运用导数,判断函数的单调性,再由单调性可证;
④根据定积分的几何意义进行判断.
解答 解:①则用反证法,假设a,b,c都不小于1,a≥1,b≥1,c≥1,则a+b+c≥3,与a+b+c<3,矛盾,故可得a,b,c中至少有一个不小于1,故①正确;
②若z为复数,且|z|=1,则由|z-i|≤|z|+|-i|=2,可得|z-i|的最大值等于2,故②正确;
③任意x∈(0,+∞),根据(x-sinx)′=1-cosx≥0,可得y=x-sinx在R上为增函数,
当x=0时,y=x-sinx=0,可得任意x∈(0,+∞),都有x-sinx>0,即x>sinx,故③正确.
④f(x)是奇函数,∴其图象关于原点对称,
∵定积分的几何意义是函数图象与x轴所围成的封闭图形的面积的代数和,
∴函数f(x)在区间[-a,a]上的图象必定关于原点O对称,
∴函数图象与x轴所围成的封闭图形的面积的代数和为0,
∴∫${\;}_{-a}^{a}$f(x)dx=0,故④错误.
故答案为:①②③.
点评 本题以命题的真假判断为载体,考查函数的单调性及应用,复数的几何意义,及定积分的几何意义,属于中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
11.若存在实数k和b,使得函数f(x)和g(x)对定义域内的任意x均满足:[f(x)-(kx+b)][g(x)-(kx+b)]≤0,且存在x1使得f(x1)-(kx1+b)=0,存在x2使得g(x2)-(kx2+b)=0,则称直线l:y=kx+b为函数f(x)和g(x)的“分界线”.在下列说法中正确的是( )
| A. | 任意两个一次函数最多存在一条“分界线” | |
| B. | “分界线”存在的两个函数的图象最多只有两个交点 | |
| C. | f(x)=x2-2x与g(x)=-x2+4的“分界线”是y=-x+2 | |
| D. | f(x)=x2与g(x)=-(x-1)2的“分界线”是y=0或$y=x-\frac{1}{2}$ |
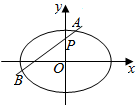 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.