题目内容
已知
cosθ+
sinθ=1,
sinθ-
cosθ=1.求证:
+
=2.
| x |
| a |
| y |
| b |
| x |
| a |
| y |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知两等式两边分别平方,相加后利用同角三角函数基本关系计算即可得证.
解答:
证明:
cosθ+
sinθ=1①,
sinθ-
cosθ=1②,
①2+②2得:
(cos2θ+sin2θ)+
(cos2θ+sin2θ)+
sinθcosθ-
sinθcosθ=
+
=2.
| x |
| a |
| y |
| b |
| x |
| a |
| y |
| b |
①2+②2得:
| x2 |
| a2 |
| y2 |
| b2 |
| 2xy |
| ab |
| 2xy |
| ab |
| x2 |
| a2 |
| y2 |
| b2 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数g(x)=asinxcosx(a>0)的最大值为
,则函数f(x)=sinx+acosx的图象的一条对称轴方程为( )
| 1 |
| 2 |
| A、x=0 | ||
B、x=-
| ||
C、x=-
| ||
D、x=-
|
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则f(x)在R上的表达式是( )
| A、y=x(x-2) |
| B、y=x(|x|-1) |
| C、y=|x|(x-2) |
| D、y=x(|x|-2) |
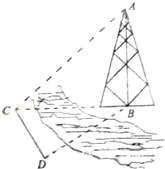 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=60°,∠BDC=75°,CD=50