题目内容
已知直线l:ax+by+1=0,圆M:x2+y2-2ax-2by=0,则直线l和圆M在同一坐标系中的图形可能是( )
A、 |
B、 |
C、 |
D、 |
考点:直线与圆的位置关系
专题:直线与圆
分析:圆M:x2+y2-2ax-2by=0的标准方程为:(x-a)2+(y-b)2=a2+b2,圆心M(a,b),半径r=
,圆心M到直线l的距离d=
>r,故直线与圆相离.由此根据四个选项利用直线和圆的性质能求出结果.
| a2+b2 |
| |a2+b2+1| | ||
|
解答:
解:圆M:x2+y2-2ax-2by=0的标准方程为:(x-a)2+(y-b)2=a2+b2,
圆心M(a,b),半径r=
,
圆心M到直线l的距离d=
>r,故直线与圆相离.
对于A,圆心M(0,b),此时a=0,直线l应该平行于x轴,故A错误;
对于B,由圆与直线有交点,知B错误;
对于C,由圆的图形得a>0,b>0,
此时直线应在第二、三、四象限,成立,故C正确;
对于D,由圆的图形得a<0,b=0,此时直线应平行于y轴,故D错误.
故选:C.
圆心M(a,b),半径r=
| a2+b2 |
圆心M到直线l的距离d=
| |a2+b2+1| | ||
|
对于A,圆心M(0,b),此时a=0,直线l应该平行于x轴,故A错误;
对于B,由圆与直线有交点,知B错误;
对于C,由圆的图形得a>0,b>0,
此时直线应在第二、三、四象限,成立,故C正确;
对于D,由圆的图形得a<0,b=0,此时直线应平行于y轴,故D错误.
故选:C.
点评:本题考查直线与圆的位置关系的应用,是中档题,解题时要注意圆的性质的合理运用.

练习册系列答案
相关题目
25人排成5×5方阵,从中选出3人分别担任队长、副队长、纪律监督员,要求这3人任两人都不同行也不同列,则不同的任职方法数为( )
| A、7200种 |
| B、1800种 |
| C、3600种 |
| D、4500种 |
已知抛物线y=ax2-2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是( )
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
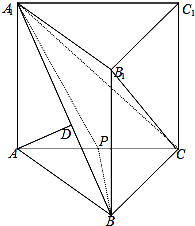 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.