题目内容

若实数a满足：a2≥3，则实数a的取值范围为
 
．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：直接求解关于a的一元二次不等式得答案．
解答： 解：由a2≥3，得a2-3≥0，即(a+
3
)(a-
3
)≥0，
解得：a≤-
3
或a≥
3
．
∴实数a的取值范围为(-∞，-
3
]∪[
3
，+∞)．
故答案为：(-∞，-
3
]∪[
3
，+∞)．
点评：本题考查了一元二次不等式的解法，是基础题．
练习册系列答案
相关题目
集合M={1，2，3，4，5}的子集是（　　）
A、15B、16C、31D、32
设f（x）=
2tx，x＜2
logt(x2-1)，x≥2
且f（2）=1，则f（1）=（　　）
A、2B、4C、6D、8
化简：2（sina）2（sinb）2+2（cosa）2（cosb）2-cos2a•cos2b=
 
．
设函数f（x）=2-
3
x
．
（Ⅰ）判断函数f（x）在（0，+∞）上的单调性并用定义加以证明；
（Ⅱ）求函数f（x）在区间[2，5]上的最大值与最小值．
若函数y=-2xm+2是正比例函数，则m的值是
 
．
不等式x2-x+1＜0的解集为
 
．
直线y=kx+b在坐标系中的位置如图，则（　　）     
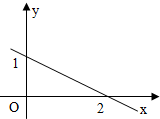
A、k=-
1
2
，b=-1
B、k=-
1
2
，b=1
C、k=
1
2
，b=-1
D、k=
1
2
，b=1
复数
3-2i
(1+i)2
（i为虚数单位）等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网