题目内容
直线l:
(t为参数),圆C:ρ=2
cos(θ+
)(极轴与x轴的非负半轴重合,且单位长度相同).
(1)求圆心C到直线l的距离;
(2)若直线l被圆C解得的弦长为
,求实数a的值.
|
| 2 |
| π |
| 4 |
(1)求圆心C到直线l的距离;
(2)若直线l被圆C解得的弦长为
6
| ||
| 6 |
考点:直线的参数方程,简单曲线的极坐标方程
专题:计算题,坐标系和参数方程
分析:(1)直线l:
(t为参数)化为普通方程,圆C:ρ=2
cos(θ+
)化为直角坐标方程,利用点到直线的距离公式,即可求圆心C到直线l的距离;
(2)根据直线l被圆C解得的弦长为
,利用勾股定理,即可求实数a的值.
|
| 2 |
| π |
| 4 |
(2)根据直线l被圆C解得的弦长为
6
| ||
| 6 |
解答:
解:(1)把
化为普通方程为x+2y+2-a=0,把ρ=2
cos(θ+
)化为直角坐标方程为x2+y2-2x+2y=0,其的圆心C的坐标为(1,-1),半径为
,
∴圆心C到直线l的距离d=
=
=
.(6分)
(2)由已知(
)2+(
)2=(
)2,∴a2-2a=0,即a=0或a=2.(10分)
|
| 2 |
| π |
| 4 |
| 2 |
∴圆心C到直线l的距离d=
| |1-2+2-a| | ||
|
| |a-1| | ||
|
| ||
| 5 |
(2)由已知(
| 3 | ||
|
| |a-1| | ||
|
| 2 |
点评:本题考查直线的参数方程、简单曲线的极坐标方程,考查直线与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若执行如图所示的框图,输入x1=1,x2=2,x3=4,x4=8,则输出的数等于( )
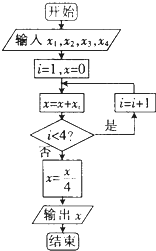

A、
| ||
B、
| ||
C、
| ||
| D、3 |
 一个底面是直角梯形的四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积和为( )
一个底面是直角梯形的四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积和为( )A、
| ||||||||
B、3
| ||||||||
C、3
| ||||||||
D、
|
设an=-n2+10n+11,则数列{an}从首项到第几项的和最大( )
| A、第10项 |
| B、第11项 |
| C、第10项或11项 |
| D、第12项 |