题目内容
在极坐标系中,已知圆ρ=
cos(θ+
)与直线
ρsin(θ+
)=a相切,求实数a的值.
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:首先把极坐标方程和直角坐标方程的互化,进一步利用点到直线的距离等于半径求出a的值.
解答:
解:已知圆ρ=
cos(θ+
),则ρ2=
ρcos(θ+
)
转化为直角坐标方程为:(x-
)2+(y+
)2=
ρsin(θ+
)=a转化为直角坐标方程为:x+y-a=0
利用圆心到直线的距离:
=
解得:a=1或-1
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
转化为直角坐标方程为:(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| π |
| 4 |
利用圆心到直线的距离:
|
| ||||
|
| ||
| 2 |
解得:a=1或-1
点评:本题考查的知识要点:极坐标方程和直角坐标方程的互化,点到直线的距离的应用及相关的运算.

练习册系列答案
相关题目
下列函数中在区间(-1,1)上既是奇函数又是增函数的为( )
| A、y=|x+1| |
| B、y=sinx |
| C、y=2x+2-x |
| D、y=lnx |
一个动点在圆x2+y2=1上移动时,它与定点(3,0)连线中点的轨迹方程是( )
| A、(x+3)2+y2=4 | ||||
| B、(X-3)2+y2=1 | ||||
C、(X+
| ||||
| D、(2x-3)2+4y2=1 |

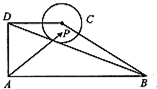 如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设
如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设