Question

已知定义在R上的函数f（x）满足：
（1）函数y=f（x）的图象关于原点对称；
（2）对任意的实数x，都有f（x+3）=f（x）成立；
（3）当x∈[0，

3

2

]时，f（x）=

3

2

-|

3

2

-2x|，
则方程f（x）=

1

|x|

在[-4，4]上根的个数是

 

．

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：由题意可得函数f（x）是奇函数，是周期等于3的周期函数，则f（x）=

1

|x|

在[-4，4]上根的个数，就是函数f（x） 与函数 y=

1

|x|

的交点的个数，结合图象得出结论．

解答： 解：∵1）函数y=f（x）的图象关于原点对称；
∴f（x）是奇函数；
∵f（x+3）=f（x）成立，∴f（x）是周期等于3的周期函数．
当x∈[0，

3

2

]时，f（x）=

3

2

-|

3

2

-2x|=

2x，0≤x≤ 3 4 3-2x， 3 4 ＜x≤ 3 2

，
则f（x）=

1

|x|

在[-4，4]上根的个数就是函数f（x） 与函数 y=

1

|x|

的交点的个数，如图所示：

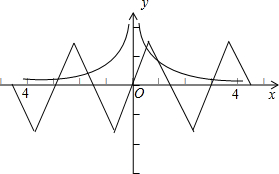
故答案为：5

点评：本题考查了函数的奇偶性、周期性以及方程的根与函数图象交点的关系；考查数形结合解决方程根的个数问题．此类问题经常考查，注意掌握．