题目内容
给出下列命题:
①α=β是tan α=tan β的既不充分也不必要条件;
②“p为真”是“p且q为真”的必要不充分条件;
③数列{an}为等比数列是数列{anan+1}为等比数列的充分不必要条件;
④a=2是f(x)=|x-a|在[2,+∞)上为增函数的充要条件.
其中真命题的序号是________.
①②③ 命题立意:本题考查充分条件、必要条件的判断,难度中等.
解题思路:对于①,当α=β= 时,不能推出tan α=tan β,反之也不成立,故①成立;对于②,易得“p为真”是“p且q为真”的必要不充分条件,故②成立;对于③,当数列{anan+1}是等比数列时不能得出数列{an}为等比数列,故③成立;对于④,a=2是f(x)=|x-a|在[2,+∞)上为增函数的充分不必要条件,故填写①②③.
时,不能推出tan α=tan β,反之也不成立,故①成立;对于②,易得“p为真”是“p且q为真”的必要不充分条件,故②成立;对于③,当数列{anan+1}是等比数列时不能得出数列{an}为等比数列,故③成立;对于④,a=2是f(x)=|x-a|在[2,+∞)上为增函数的充分不必要条件,故填写①②③.

练习册系列答案
相关题目
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:
| 8 | 7 | 7 | |||||
| 9 | 4 | 0 | 1 | 0 | x | 9 | 1 |
则7个剩余分数的方差为________.
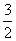 a2 B.
a2 B.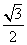 a2
a2 a2 D.
a2 D. a2
a2
