题目内容
已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈({0,
),不等式f(x)+2<1ogax恒成立时,实数a的取值范围是( )
| 1 |
| 2 |
A、(
| |||||
B、[
| |||||
C、(
| |||||
D、[
|
考点:抽象函数及其应用,函数恒成立问题
专题:函数的性质及应用
分析:根据抽象函数的定义,利用赋值法求出函数f(x)的表达式,然后根据不等式恒成立,结合对数函数的性质即可得到结论.
解答:
解:∵f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,
∴令y=0,x=1代入已知式子f(x+y)-f(y)=(x+2y+1)x,
得f(1)-f(0)=2,
∵f(1)=0,
∴f(0)=-2;
令y=0得f(x)+2=(x+1)x,
∴f(x)=x2+x-2.
当x∈(0,
),不等式f(x)+2<logax恒成立时,
即x2+x<logax恒成立,
设g(x)=x2+x,在(0,
)上是增函数,
∴0<g(x)<
,
∴要使x2+x<logax恒成立,
则logax≥
在x∈(0,
)恒成立,
若a>1时,不成立.
若0<a<1,则有loga
=
时,a=
,
∴要使logax≥
在x∈(0,
)恒成立,
则
≤a<1,即[
,1),
故选:D.
∴令y=0,x=1代入已知式子f(x+y)-f(y)=(x+2y+1)x,
得f(1)-f(0)=2,
∵f(1)=0,
∴f(0)=-2;
令y=0得f(x)+2=(x+1)x,
∴f(x)=x2+x-2.
当x∈(0,
| 1 |
| 2 |
即x2+x<logax恒成立,
设g(x)=x2+x,在(0,
| 1 |
| 2 |
∴0<g(x)<
| 3 |
| 4 |
∴要使x2+x<logax恒成立,
则logax≥
| 3 |
| 4 |
| 1 |
| 2 |
若a>1时,不成立.
若0<a<1,则有loga
| 1 |
| 2 |
| 3 |
| 4 |
| |||
| 4 |
∴要使logax≥
| 3 |
| 4 |
| 1 |
| 2 |
则
| |||
| 4 |
| |||
| 4 |
故选:D.
点评:本题主要考查抽象函数的应用,利用赋值法是解决抽象函数的基本方法,将不等式恒成立转化为求函数最值问题是解决此类问题的基本方法.

练习册系列答案
相关题目
设函数f1(x)=log4x-(
)x、f2(x)=log
x-(
)x的零点分别为x1、x2,则( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、x1x2≥2 |
| B、1<x1x2<2 |
| C、x1x2=1 |
| D、0<x1x2<1 |
某几何体的三视图如图所示,它的体积为( )
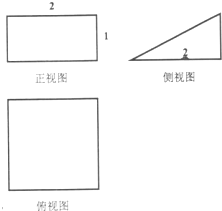

| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
设随机变量X~N(1,52),且P(X≤0)=P(X>a-2),则实数a的值为( )
| A、4 | B、6 | C、8 | D、10 |
函数y=cos2ax-sin2ax的最小正周期为π,则a的值是( )
| A、-1 | B、1 | C、2 | D、±1 |
在等差数列{an}中,a6=a3+a8,a5=( )
| A、-1 | B、0 | C、1 | D、以上都不对 |
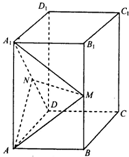 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.