题目内容
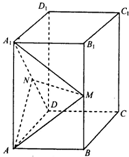 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.(1)求直线MN与平面ADD1A1所成角的正切值大小与三棱椎A1-AMN的体积;
(2)求证直线MN∥平面A1B1C1D1.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AA1中点P,连结PM,PN.∠PNM为直线MN与平面ADD1A1所成的角,由此能求出直线MN与平面ADD1A1所成的角的正切值.由VA1-AMN=VM-A1AN,利用等积法能求出三棱椎A1-AMN的体积.
(2)设DD1的中点为P,连PN,PM,由中位线的性质得PN∥A1D1,PM∥D1B1,由此能证明直线MN∥平面A1B1C1D1.
(2)设DD1的中点为P,连PN,PM,由中位线的性质得PN∥A1D1,PM∥D1B1,由此能证明直线MN∥平面A1B1C1D1.
解答:
(本小题满分12分)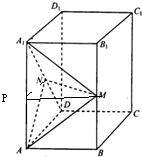
(Ⅰ)解:取AA1中点P,连结PM,PN.
则MP⊥面ADD1A1.
所以∠PNM为直线MN与平面ADD1A1所成的角.…(2分)
在Rt△PMN中,知PM=1,PN=
,
∴tan∠PMN=
=2,
故直线MN与平面ADD1A1所成的角的正切值为2.…(4分)
S△A1AN=
S△A1AD=
×
×1×2=
,
VA1-AMN=VM-A1AN=
×S△A1AN×AB=
.(8分)
(2)证明:设DD1的中点为P,连PN,PM,
由中位线的性质得PN∥A1D1,PM∥D1B1,
所以平面PMN∥平面A1B1C1D1,直线MN?平面PMN,
直线MN∥平面A1B1C1D1.(12分)

(Ⅰ)解:取AA1中点P,连结PM,PN.
则MP⊥面ADD1A1.
所以∠PNM为直线MN与平面ADD1A1所成的角.…(2分)
在Rt△PMN中,知PM=1,PN=
| 1 |
| 2 |
∴tan∠PMN=
| PM |
| PN |
故直线MN与平面ADD1A1所成的角的正切值为2.…(4分)
S△A1AN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
VA1-AMN=VM-A1AN=
| 1 |
| 3 |
| 1 |
| 6 |
(2)证明:设DD1的中点为P,连PN,PM,
由中位线的性质得PN∥A1D1,PM∥D1B1,
所以平面PMN∥平面A1B1C1D1,直线MN?平面PMN,
直线MN∥平面A1B1C1D1.(12分)
点评:本题考查直线MN与平面ADD1A1所成角的正切值大小与三棱椎A1-AMN的体积的求法,考查直线与平面平行的证明,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
若函数f(x)=|ax+x2-xlna-t|-1(a>1)有三个零点,则t的值是( )
| A、2 | B、4 | C、8 | D、0 |
设
=(t,1)(t∈Z),
=(2,4),满足|
|≤4,则△OAB为直角三角形的概率是( )
| OA |
| OB |
| OA |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈({0,
),不等式f(x)+2<1ogax恒成立时,实数a的取值范围是( )
| 1 |
| 2 |
A、(
| |||||
B、[
| |||||
C、(
| |||||
D、[
|
 如图,在平面直角坐标系中,正方形OABC的边长为1,E为AB的中点,若F为正方形内(含边界)任意一点,则
如图,在平面直角坐标系中,正方形OABC的边长为1,E为AB的中点,若F为正方形内(含边界)任意一点,则