题目内容
已知O是坐标原点,A(-1,1),若点M(x,y)为平面区域
上的一个动点,则
•
的最小值是( )
|
| OA |
| OM |
| A、-1 | B、0 | C、1 | D、2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用向量数量积的坐标公式,以及目标函数的几何意义,进行求最值即可.
解答:
解:作出不等式组对应的平面区域如图:
设z=
•
,
则z=(-1,1)•(x,y)=-x+y,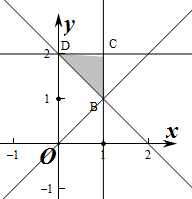
由z=-x+y,得y=x+z表示,斜率为1纵截距为z的一组平行直线,
平移直线y=x+z,当直线y=x+z经过点B时,直线y=x+z的截距最小,此时z最小,
由
,解得
,即B(1,1),此时zmin=-1+1=0.
即
•
的最小值0,
故选:B
设z=
| OA |
| OM |
则z=(-1,1)•(x,y)=-x+y,

由z=-x+y,得y=x+z表示,斜率为1纵截距为z的一组平行直线,
平移直线y=x+z,当直线y=x+z经过点B时,直线y=x+z的截距最小,此时z最小,
由
|
|
即
| OA |
| OM |
故选:B
点评:本题主要考查线性规划的基本应用,利用z的几何意义以及向量的数量积的坐标运算是解决线性规划问题的关键,注意利用数形结合来解决.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
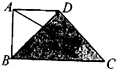 如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有
如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有| PA |
| BD |
A、[-
| ||
B、[-1,
| ||
| C、[-1,1] | ||
| D、[-1,0] |
设变量x、y满足约束条件
,则z=2x×(
)y的最小值为( )
|
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
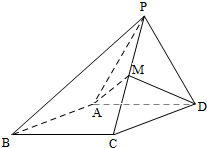 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.