题目内容
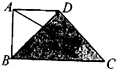如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有| PA |
| BD |
A、[-
| ||
B、[-1，
| ||
| C、[-1，1] | ||
| D、[-1，0] |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：在直角梯形ABCD中，DA=AB=1，BC=2，由此求得BD，进一步利用向量的三角形法则以及向量的运算得到
•
的最值．
| PA |
| BD |
解答：
解：∵在直角梯形ABCD中，DA=AB=1，BC=2，
∴BD=
．
如图所示，过点A作AO⊥BD，垂足为O．
则
=
+
，
•
=0．
∴
•
=（
+
）•
=
•
．
所以当点P取点B时，则
•
=
•
=
×
×
=1，
当点P取BC边上的任意一点时，
•
取得最小值=-
×
×
=-1．
∴
•
的取值范围是[-1，1]．
故选C．．
∴BD=
| 2 |
如图所示，过点A作AO⊥BD，垂足为O．
则
| PA |
| PO |
| OA |
| OA |
| BD |
∴
| PA |
| BD |
| PO |
| OA |
| BD |
| PO |
| BD |
所以当点P取点B时，则
| PA |
| BD |
| PO |
| BD |
| 1 |
| 2 |
| 2 |
| 2 |
当点P取BC边上的任意一点时，
| PA |
| BD |
| 1 |
| 2 |
| 2 |
| 2 |
∴
| PA |
| BD |
故选C．．
点评：本题考查了向量的数量积定义及其性质、投影的定义、向量的三角形法则、直角梯形的性质等基础知识与基本技能方法，考查了转化方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
2014年11月10日APEC会议在北京召开，某服务部需从大学生中招收志愿者，被招收的志愿者需参加笔试和面试两部分，把参加笔试的40名大学生的成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100），得到的频率分布直方图如图所示：