题目内容
一组数据4、7、10、6、9,n是这组数据的中位数,设f(x)=(
-x2)n.
(1)求f(x)的展开式中x-1的项的系数;
(2)求f(x)的展开式中系数最大的项和系数最小的项.
| 1 |
| x |
(1)求f(x)的展开式中x-1的项的系数;
(2)求f(x)的展开式中系数最大的项和系数最小的项.
考点:二项式系数的性质
专题:计算题,二项式定理
分析:(1)依题意有:这组数据的中位数是7,即n=7,可得f(x)的展开式的通项Tr+1,令x的指数为-1,即可求f(x)的展开式中x-1的项的系数;
(2)f(x)的展开式中共8项,其中第4项和第5项的二项式系数最大,而第5项的系数等于第5项二项式系数,第4项的系数等于第4项二项式系数的相反数,即可求f(x)的展开式中系数最大的项和系数最小的项.
(2)f(x)的展开式中共8项,其中第4项和第5项的二项式系数最大,而第5项的系数等于第5项二项式系数,第4项的系数等于第4项二项式系数的相反数,即可求f(x)的展开式中系数最大的项和系数最小的项.
解答:
解:(1)依题意有:这组数据的中位数是7,即n=7,
故f(x)的展开式中Tr+1=
(x-1)7-r(-x2)r=
(-1)rx3r-7,
由3r-7=-1可知r=2,故展开式中x-1的项的系数为
(-1)2=21(6分);
(2)f(x)的展开式中共8项,其中第4项和第5项的二项式系数最大,
而第5项的系数等于第5项二项式系数,故第5项的系数最大,
即最大项为T5
(x-1)3(-x2)4=35x5,第4项的系数等于第4项二项式系数的相反数,
故第4项的系数最小,即最小项为T4
(x-1)4(-x2)3=-35x2(12分)
故f(x)的展开式中Tr+1=
| C | r 7 |
| C | r 7 |
由3r-7=-1可知r=2,故展开式中x-1的项的系数为
| C | 2 7 |
(2)f(x)的展开式中共8项,其中第4项和第5项的二项式系数最大,
而第5项的系数等于第5项二项式系数,故第5项的系数最大,
即最大项为T5
| =C | 4 7 |
故第4项的系数最小,即最小项为T4
| =C | 3 7 |
点评:本题考查二项式定理的运用,考查展开式中的系数,确定展开式的通项是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某单位有老年人27人,中年人54人,青年人81人,为了调查他们身体状况的某项指标,需从他们中抽取一个容量为36的样本,适合抽取样本的方法是( )
| A、抽签法 | B、系统抽样 |
| C、随机数表法 | D、分层抽样 |
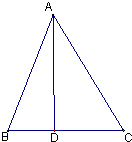 在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC
在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC 如图△ABC为直角三形,
如图△ABC为直角三形,