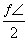题目内容
已知函数f(x)＝ax2＋blnx在x＝1处有极值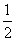
.
(1)求a，b的值；
(2)判断函数y＝f(x)的单调性并求出单调区间．
解析 (1)因为函数f(x)＝ax2＋blnx，
所以f′(x)＝2ax＋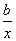
.
又函数f(x)在x＝1处有极值，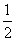
所以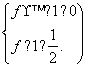
即
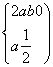解得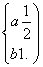
(2)由(1)可知f(x)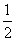＝x2－lnx，其定义域是(0，＋∞)，且f′(x)＝x－
＝
.
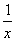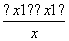当x变化时，f′(x)，f(x)的变化情况如下表：
| x | (0,1) | 1 | (1，＋∞) |
| f′(x) | － | 0 | ＋ |
| f(x) | 极小值 |
练习册系列答案
阅读快车系列答案
相关题目
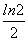D．ln 2
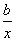，曲线y＝f(x)在点(2，f(2))处的切线方程为7x－4y－12＝0.
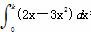＝0，则k等于_________．
tan x)cos x的最小正周期为( )．
C．π D.