题目内容
设函数f(x)=ax-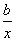 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
解析 (1)方程7x-4y-12=0可化为y=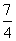 x-3,
x-3,
当x=2时,y=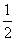 .又f′(x)=a+
.又f′(x)=a+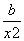 ,于是
,于是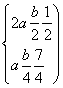
解得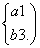 故f(x)=x-
故f(x)=x-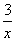 .
.
(2)证明 设P(x0,y0)为曲线上任一点,
由f′(x)=1+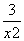 知,曲线在点P(x0,y0)处的切线方程为y-y0=
知,曲线在点P(x0,y0)处的切线方程为y-y0=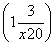 (x-x0),
(x-x0),
即y-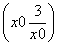 =
=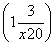 (x-x0).
(x-x0).
令x=0得,y=-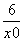 ,从而得切线与直线x=0交点坐标为
,从而得切线与直线x=0交点坐标为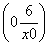 .
.
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为
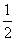
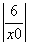 |2x0|=6.
|2x0|=6.
故曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,此定值为6.

练习册系列答案
相关题目
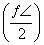 sin x+cos x,则f
sin x+cos x,则f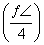 =________.
=________.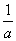 处有极值,则ab的值为( )
处有极值,则ab的值为( )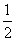 .
.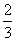 时,y=f(x)有极值.
时,y=f(x)有极值. B.1-
B.1-