题目内容
若f(2x+1)=x2-1,则f(0)=( )
A、-
| ||
| B、0 | ||
C、
| ||
| D、-1 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:令x=-
代入f(2x+1)=x2-1,即可得出f(0)的值.
| 1 |
| 2 |
解答:
解:令x=-
代入f(2x+1)=x2-1,
f(0)=(-
)2-1=-
,
故选:A.
| 1 |
| 2 |
f(0)=(-
| 1 |
| 2 |
| 3 |
| 4 |
故选:A.
点评:本题主要考查函数的解析式的用法,即已知函数的表达式,可求任一点的函数值.本题属于低档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列说法正确的是( )
| A、数列1,0,-1,-2与数列-2,-1,0,1是相同的数列 | ||||||||
| B、数列0,2,4,6,8,…,可记为{2n},n∈N+ | ||||||||
C、数列{
| ||||||||
D、数列
|
若函数f(x)=2-|x|-c的图象与x轴有公共点,则实数c的职值范围是( )
| A、[一1,0) |
| B、[0,1] |
| C、(0,1] |
| D、[1,+∞) |
如图的程序运行后,输出a的值是( )


| A、8 | B、7 | C、6 | D、4 |
下列各组对象可构成一个集合的是( )
| A、与10非常接近的数 |
| B、我校学生中的女生 |
| C、中国漂亮的工艺品 |
| D、本班视力差的女生 |
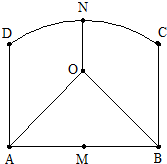 为丰富农村业余文化生活,决定在A,B,N三个村子的中间地带建造文化中心.通过测量,发现三个村子分别位于矩形ABCD的两个顶点A,B和以边AB的中心M为圆心,以MC长为半径的圆弧的中心N处,且AB=8km,BC=4
为丰富农村业余文化生活,决定在A,B,N三个村子的中间地带建造文化中心.通过测量,发现三个村子分别位于矩形ABCD的两个顶点A,B和以边AB的中心M为圆心,以MC长为半径的圆弧的中心N处,且AB=8km,BC=4 若f(x)是R上的奇函数,在[0,+∞)上图象如图所示,则满足f(x-1)>0的x的集合是
若f(x)是R上的奇函数,在[0,+∞)上图象如图所示,则满足f(x-1)>0的x的集合是