关于x.y的不等式组$\left\{\begin{array}{l}x+y-3≥0\\ x-2y+3≥0\\ x-2≤0\end{array}\right.$.表示的区域为D.若区域D内存在满足t≤3x-y的点.则实数t的取值范围为( )A．(-∞.1]B．[1.+∞)C．(-∞.5]D．[5.+∞) 题目和参考答案——青夏教育精英家教网—

题目内容

5．关于x，y的不等式组$\left\{\begin{array}{l}x+y-3≥0\\ x-2y+3≥0\\ x-2≤0\end{array}\right.$，表示的区域为D，若区域D内存在满足t≤3x-y的点，则实数t的取值范围为（　　）

A．

（-∞，1]

B．

[1，+∞）

C．

（-∞，5]

D．

[5，+∞）

分析首先画出可行域，利用z=3x-y的几何意义求出z 的最大值，根据区域D内存在满足t≤3x-y的点，只要t≤（3x-y）_max即可．

解答解：由已知得到平面区域如图：区域D内存在满足t≤3x-y的点，即区域D内存在满足t≤（3x-y）_max，
由题意，当直线y=3x-z经过图中A（2，1）时，使得3x-y最大，最大为2×3-1=5，
所以t≤5；
故选：C．

点评本题考查的知识点是简单线性规划的应用．我们在解决线性规划的小题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证，求出最优解．

练习册系列答案

16．已知抛物线C：y²=2px（p＞0）的焦点F，准线l，点A为C上一点，以F为圆心，FA为半径作圆交l于B、D两点，∠BFD=120°，△ABD的面积为4$\sqrt{3}$，则p的值为（　　）

13．已知函数f（x）=x-alnx，a∈R．
（Ⅰ）研究函数f（x）的单调性；
（Ⅱ）设函数f（x）有两个不同的零点x₁、x₂，且x₁＜x₂．
（1）求a的取值范围；
（2）求证：x₁x₂＞e²．

20．已知i是虚数单位，若z（1+i）=1+3i，则$\overline z$=（　　）

10．

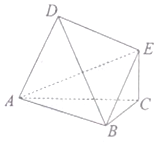如图△ABC和△ABD均为等腰直角三角形，AD⊥BD，AC⊥BC，平面ABC⊥平面ABD，EC⊥平面ABC，EC=1，$AD=2\sqrt{2}$．
（1）证明：DE⊥AB；
（2）求二面角D-BE-A的余弦值．

17．已知向量$\overrightarrow a$与$\overrightarrow b$满足$|{\overrightarrow a}|=2|{\overrightarrow b}|$，若向量$\overrightarrow c=\overrightarrow a+\overrightarrow b$，且$\overrightarrow c⊥\overrightarrow b$，则$\overrightarrow a$与$\overrightarrow b$的夹角为120°．

12．

已知四棱锥的正视图与俯视图如图所示，该四棱锥的体积为24，则四棱锥的侧视图面积为6，四棱锥的表面积为60．

13．

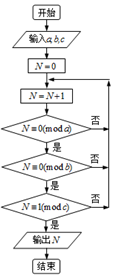若正整数N除以正整数m后的余数为n，则记为N≡n（bmodm），例如10≡4（bmod6），如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节，执行该框图，输入a=2，b=3，c=5，则输出的N=（　　）

试题分类