题目内容
17.已知向量$\overrightarrow a$与$\overrightarrow b$满足$|{\overrightarrow a}|=2|{\overrightarrow b}|$,若向量$\overrightarrow c=\overrightarrow a+\overrightarrow b$,且$\overrightarrow c⊥\overrightarrow b$,则$\overrightarrow a$与$\overrightarrow b$的夹角为120°.分析 设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,根据向量的垂直即可得到cosθ=-$\frac{1}{2}$,问题得以解决.
解答 解:设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,
∵向量$\overrightarrow c=\overrightarrow a+\overrightarrow b$,且$\overrightarrow c⊥\overrightarrow b$,向量$\overrightarrow a$与$\overrightarrow b$满足$|{\overrightarrow a}|=2|{\overrightarrow b}|$,
∴$\overrightarrow{c}$•$\overrightarrow{b}$=($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cosθ+${\overrightarrow{b}}^{2}$=0,
即cosθ=-$\frac{1}{2}$,
∵0≤θ≤π.
∴θ=120°,
故答案为:120°.
点评 本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
7.设a,b是两条直线,α,β是两个平面,则a∥b的一个充分条件是( )
| A. | a⊥α,b∥β,α⊥β | B. | a?α,b⊥β,α∥β | C. | a⊥α,b⊥β,α∥β | D. | a?α,b∥β,α⊥β |
5.关于x,y的不等式组$\left\{\begin{array}{l}x+y-3≥0\\ x-2y+3≥0\\ x-2≤0\end{array}\right.$,表示的区域为D,若区域D内存在满足t≤3x-y的点,则实数t的取值范围为( )
| A. | (-∞,1] | B. | [1,+∞) | C. | (-∞,5] | D. | [5,+∞) |
4.执行如图所示的程序框图,若输入的k,b,r的值分别为2,2,4,则输出i的值是( )
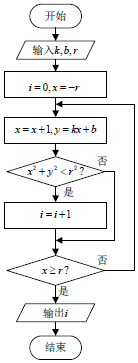

| A. | 4 | B. | 3 | C. | 6 | D. | 7 |
5.设函数f(x)=|x2-2x-1|,若m>n>1,且f(m)=f(n),则(m-1)(n-1)的取值范围为( )
| A. | (0,2) | B. | (0,2] | C. | (1,2) | D. | (1,2] |