题目内容
16.已知抛物线C:y2=2px(p>0)的焦点F,准线l,点A为C上一点,以F为圆心,FA为半径作圆交l于B、D两点,∠BFD=120°,△ABD的面积为4$\sqrt{3}$,则p的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据∠BFD,|BF|=|FD|,推断出∠FBD=∠FBD=30°,进而表示出|FR|,|BF|,|BR|,|DF|,|DR|,进而表示出|BD|及圆的半径,进而利用抛物线的定义求得A到直线l的距离,利用三角形的面积,求得p的值.
解答 解:∵∠BFD=120°,|BF|=|FD|,
∴∠FBD=∠FBD=30°,
∵在Rt△BFR中,|FR|=p,
∴|BF|=2p,|BR|=$\sqrt{3}$p,
同理得:|DF|=2p,|DR|=$\sqrt{3}$p,
∴|BD|=|BR|+|RD|=2$\sqrt{3}$P,
圆F的半径|FA|=|FB|=2p,
由抛物线的定义可知A到l的距离d=|FA|=2p,
∵△ABD的面积为4$\sqrt{3}$,
∴$\frac{1}{2}$|BD|•d=4$\sqrt{3}$,即$\frac{1}{2}$•2$\sqrt{3}$p•2p=4$\sqrt{3}$,解得:p=$\sqrt{2}$或p=-$\sqrt{2}$(舍去),
p的值为$\sqrt{2}$,
故选B.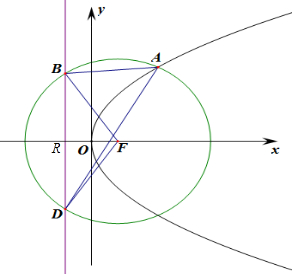
点评 本题主要考查了抛物线的基本性质,圆锥曲线的位置关系,圆的方程等问题.综合性强,计算量大,考查了学生分析推理和运算的能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
7.设a,b是两条直线,α,β是两个平面,则a∥b的一个充分条件是( )
| A. | a⊥α,b∥β,α⊥β | B. | a?α,b⊥β,α∥β | C. | a⊥α,b⊥β,α∥β | D. | a?α,b∥β,α⊥β |
4.${(2x-\frac{1}{2x})^{10}}$的常数项为( )
| A. | -252 | B. | 252 | C. | -210 | D. | 210 |
11.设集合A={x|x2-1<0},B={x|y=ln(x-1)},则A∪B=( )
| A. | (-1,1) | B. | (-1,+∞) | C. | (-1,1)∪(1,+∞) | D. | (1,+∞) |
5.关于x,y的不等式组$\left\{\begin{array}{l}x+y-3≥0\\ x-2y+3≥0\\ x-2≤0\end{array}\right.$,表示的区域为D,若区域D内存在满足t≤3x-y的点,则实数t的取值范围为( )
| A. | (-∞,1] | B. | [1,+∞) | C. | (-∞,5] | D. | [5,+∞) |
4.执行如图所示的程序框图,若输入的k,b,r的值分别为2,2,4,则输出i的值是( )
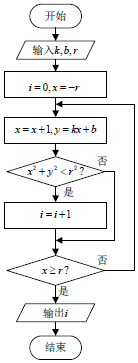

| A. | 4 | B. | 3 | C. | 6 | D. | 7 |