题目内容
沿一条小路前进,从A到B,方位角是50°,距离是470m,从B到C,方位角是80°,距离是860m,从C到D,方位角是150°,距离是640m.试画出示意图,并计算出从A到D的方位角和距离.
考点:解三角形的实际应用
专题:应用题,解三角形
分析:从A到D的方位角,需构造三角形,连结AC,在△ABC中,用余弦定理求出AC,进而求出∠BAC,再在△ACD中,求出AD和∠CAD.
解答:
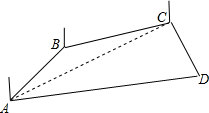 解:示意图如图所示,连结AC,
解:示意图如图所示,连结AC,
在△ABC中,∠ABC=50°+(180°-80°)=150°,
由余弦定理,得AC=
=
.
由正弦定理,利用计算器可得∠BAC≈19.5°,∠ACB=10.5°.
在△ACD中,∠ACD=80°-10.5°+30°=99.5°.
由余弦定理,得AD≈1531.
由正弦定理,得∠CAD≈24.4°.
∴从A到D的方位角为50°+19.5°+24.4°=93.9°,
即A到D的方位角为93.9°,距离为1531 m.
 解:示意图如图所示,连结AC,
解:示意图如图所示,连结AC,在△ABC中,∠ABC=50°+(180°-80°)=150°,
由余弦定理,得AC=
4702+8602-2×470×860×(-
|
960500+404200
|
由正弦定理,利用计算器可得∠BAC≈19.5°,∠ACB=10.5°.
在△ACD中,∠ACD=80°-10.5°+30°=99.5°.
由余弦定理,得AD≈1531.
由正弦定理,得∠CAD≈24.4°.
∴从A到D的方位角为50°+19.5°+24.4°=93.9°,
即A到D的方位角为93.9°,距离为1531 m.
点评:明确方位角的定义,是由指北方向顺时针到目标方向线的水平角.本题中A到D的方位角是50°+∠BAD,把角的求解放到三角形中,关键是理顺题目中的数量关系,结合示意图,构造出相应的三角形,结合正、余弦定理解决.

练习册系列答案
相关题目
如图,在△ABC中,P为中线AO上一个动点,若AO=2,则
•(
+
)的最小值是( )

| PA |
| PB |
| PC |

| A、-2 | ||
| B、-1 | ||
C、-
| ||
| D、0 |
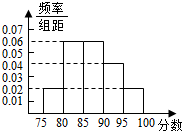 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):