题目内容
18.已知数列{an}是等差数列,首项a1=2,且a3是a2与a4+1的等比中项.(1)求数列{an}的通项公式;
(2)设bn=$\frac{2}{(n+3)({a}_{n}+2)}$,求数列{bn}的前n项和Sn.
分析 (1)设等差数列的公差为d,首项a1=2,且a3是a2与a4+1的等比中项即可求出公差d,再写出通项公式即可,
(2)化简bn根据式子的特点进行裂项,再代入数列{bn}的前n项和Sn,利用裂项相消法求出Sn.
解答 解:(1)设等差数列{an}的公差为d,由a1=2,且a3是a2与a4+1的等比中项.
∴(2+2d)2=(3+3d)(2+d),
解得d=2,
∴an=a1+(n-1)d=2+2(n-1)=2n,
(2)bn=$\frac{2}{(n+3)({a}_{n}+2)}$=$\frac{2}{(n+3)(2n+2)}$=$\frac{1}{(n+1)(n+3)}$=$\frac{1}{2}$($\frac{1}{n+1}$-$\frac{1}{n+3}$),
∴Sn=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$+$\frac{1}{n+1}$-$\frac{1}{n+3}$)=$\frac{1}{2}$($\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$)=$\frac{5}{12}$-$\frac{2n+5}{2(n+2)(n+3)}$
点评 本题考查了等差数列的通项公式及前n项和公式,以及裂项相消法求数列的前n项和,考查了基础知识和运算能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.将一根长为10米的木棒截成三段,则每段木棒长不低于1米的概率为( )
| A. | $\frac{8}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{49}{100}$ | D. | $\frac{49}{200}$ |
6.四面体A-BCD中,AB=CD=10,AC=BD=2$\sqrt{34}$,AD=BC=2$\sqrt{41}$,则四面体A-BCD外接球的表面积为( )
| A. | 50π | B. | 100π | C. | 200π | D. | 300π |
10.已知数据x,y的取值如表:
从散点图可知,y与x呈线性相关关系,已知第四组数据在回归直线$\hat y=0.8x+\hat a$上,则m的取值为13.8.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 13.2 | m | 14.2 | 15.4 | 16.4 |
7.已知z=x2+y2,其中实数x,y满足$\left\{\begin{array}{l}-x+y≤1\\ x+2y≥2\\ x-2≤0\end{array}\right.$,则z的最小值是( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{7}{9}$ | C. | $\frac{4}{5}$ | D. | $\sqrt{13}$ |
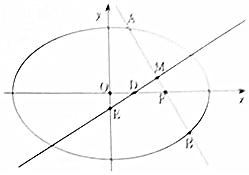 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.