题目内容
17.某几何体的三视图如图所示,则该几何体的表面积为16+2$\sqrt{3}$+2$\sqrt{5}$;体积为$\frac{20}{3}$.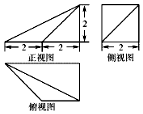
分析 由三视图知该几何体是四棱锥与三棱锥的组合体,结合图中数据求出它的表面积和体积.
解答 解:由三视图可知:该几何体是四棱锥与三棱锥的组合体,如图所示;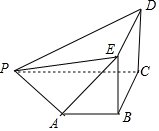
则它的表面积为
S=S正方形BCDE+S梯形PABC+S△EAB+S△PAE+S△PDE+S△PCD
=22+$\frac{1}{2}$×(2+4)×2+$\frac{1}{2}$×2×2+$\frac{1}{2}$×2$\sqrt{6}$×$\sqrt{2}$+$\frac{1}{2}$×2$\sqrt{5}$×2+$\frac{1}{2}$×4×2
=16+2$\sqrt{3}$+2$\sqrt{5}$;
体积为V=V四棱锥E-PABC+V三棱锥P-CDE
=$\frac{1}{3}$×6×2+$\frac{1}{3}$×$\frac{1}{2}$×22×4
=$\frac{20}{3}$.
故答案为:16+2$\sqrt{3}$+2$\sqrt{5}$,$\frac{20}{3}$.
点评 本题考查了几何体三视图的应用问题,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.若$\overrightarrow i=(1,0)、\overrightarrow j=(0,1)$,则与$2\overrightarrow i+3\overrightarrow j$垂直的向量是( )
| A. | $3\overrightarrow i+2\overrightarrow j$ | B. | $-2\overrightarrow i+3\overrightarrow j$ | C. | $-3\overrightarrow i+2\overrightarrow j$ | D. | $2\overrightarrow i-3\overrightarrow j$ |
10.下列说法正确的是( )
| A. | “x2+x-2>0”是“x>1”的充分不必要条件 | |
| B. | 命题“?x∈R,使得2x2-1<0”的否定是“?x∈R,均有2x2-1>0” | |
| C. | “若am2<bm2,则a<b”的逆否命题为真命题 | |
| D. | 命题“若$x=\frac{π}{4},则tanx=1$”的逆命题为真命题 |
 我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.
我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.