题目内容
4．求函数f（x）=x2+x在区间[x0，x0+△x]上的平均变化率，并求当x0=1，△x=0.1时的平均变化率．分析 利用平均变化率的意义即可得出．
解答 解：△y=（x0+△x）2+（x0+△x]-x02-x0=（2x0+1）△x+△x2，
∴$\frac{△y}{△x}$=2x0+1+△x，
当x0=1时，平均变化率为3+△x，
当x0=0.1时，平均变化率为1.2+△x
点评 本题考查了平均变化率的意义及其求法，属于基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
6．
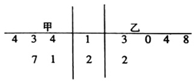2017年3月2日至16日，全国两会在北京召开，甲、乙两市近5年与会代表名额数统计如图所示，设甲、乙的数据平均数分别为$\overline{{x}_{1}}$，$\overline{{x}_{2}}$，中位数分别为y1，y2，则（ ）
2017年3月2日至16日，全国两会在北京召开，甲、乙两市近5年与会代表名额数统计如图所示，设甲、乙的数据平均数分别为$\overline{{x}_{1}}$，$\overline{{x}_{2}}$，中位数分别为y1，y2，则（ ）| A． | $\overline{{x}_{1}}$＞$\overline{{x}_{2}}$，y1＞y2 | B． | $\overline{{x}_{1}}$＞$\overline{{x}_{2}}$，y1=y2 | C． | $\overline{{x}_{1}}$＜$\overline{{x}_{2}}$，y1=y2 | D． | $\overline{{x}_{1}}$＜$\overline{{x}_{2}}$，y1＜y2 |
7．已知全集U={x∈N|x≤4}，A={0，1，3}，B={1，3，4}，则∁U（A∩B）=（ ）
| A． | {2} | B． | {4} | C． | {2，4} | D． | {0，2，4} |
4．已知函数f（x）是R上的奇函数，当x＞0时，f（x）=ex+x2，则不等式f（3-x2）＞f（2x）的解集为（ ）
| A． | （-3，1） | B． | （-1，3） | C． | （-∞，-3）∪（1，+∞） | D． | （-∞，-，1）∪（3，+∞） |
11．已知函数f（x）=$\left\{\begin{array}{l}1-|x+1|，x＜1\\{x^2}-4x+2，x≥1\end{array}$，则函数g（x）=2|x|f（x）-2的零点个数为（ ）个．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
9．若f（tanx）=sinxcosx，则f（2）的值是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{5}$ | D． | $\frac{2}{3}$ |
14．由曲线y=x2+1、直线y=-x+3，x轴与y轴所围成图形的面积为（ ）
| A． | 3 | B． | $\frac{10}{3}$ | C． | $\frac{7}{3}$ | D． | $\frac{8}{3}$ |