题目内容
已知函数f(x)=
,其中x∈[3,5].
(Ⅰ)用定义证明函数f(x)在[3,5]上单调递减;
(Ⅱ)结合单调性,求函数f(x)=
在区间[3,5]上的最大值和最小值.
| x+1 |
| x-2 |
(Ⅰ)用定义证明函数f(x)在[3,5]上单调递减;
(Ⅱ)结合单调性,求函数f(x)=
| x+1 |
| x-2 |
考点:函数的最值及其几何意义,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)用定义法证明单调性一般可以分为五步,取值,作差,化简变形,判号,下结论.
(2)由单调性求最值.
(2)由单调性求最值.
解答:
解:(Ⅰ)证明:任取x1,x2∈[3,5],且x1<x2,则
f(x1)-f(x2)=
-
=
;
∵x1,x2∈[3,5],且x1<x2,
∴x1-2>0,x2-2>0,x2-x1>0;
故f(x1)-f(x2)>0;
故函数f(x)在[3,5]上单调递减;
(Ⅱ)由(Ⅰ)知,
函数f(x)=
在区间[3,5]上的最大值为f(3)=
=4;
最小值为f(5)=
=2.
f(x1)-f(x2)=
| x1+1 |
| x1-2 |
| x2+1 |
| x2-2 |
| 3(x2-x1) |
| (x1-2)(x2-2) |
∵x1,x2∈[3,5],且x1<x2,
∴x1-2>0,x2-2>0,x2-x1>0;
故f(x1)-f(x2)>0;
故函数f(x)在[3,5]上单调递减;
(Ⅱ)由(Ⅰ)知,
函数f(x)=
| x+1 |
| x-2 |
| 3+1 |
| 3-2 |
最小值为f(5)=
| 5+1 |
| 5-2 |
点评:本题考查了函数单调性的证明,一般有两种方法,定义法,导数法,同时考查了函数的最值,属于中档题.

练习册系列答案
相关题目
已知正四棱锥S-ABCD中,SA=2
,那么当该棱锥的体积最大时,它的底面积为( )
| 3 |
| A、4 | B、8 | C、16 | D、32 |
已知集合A={0,1,2},集合B={0,2,4},则A∪B=( )
| A、{0} |
| B、{2} |
| C、{0,2,4} |
| D、{0,1,2,4} |
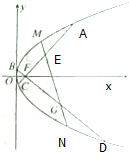 如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且
如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且