题目内容
7.已知二次函数f(x)=x2+mx-3的两个零点为-1和n,(Ⅰ)求m,n的值;
(Ⅱ)若f(3)=f(2a-3),求a的值.
分析 (Ⅰ)利用函数的零点与方程根的关系,列出方程求解即可得到m,n的值;
(Ⅱ)通过f(3)=f(2a-3),利用二次函数的对称性即可求a的值.
解答 解:(Ⅰ)因为二次函数二次函数f(x)=x2+mx-3的两个零点为-1和n,
所以,-1和n是方程x2+mx-3=0的两个根.
则-1+n=-m,-1×n=-3,--------------------------(4分)
所以m=-2,n=3.--------------------------(6分)
(Ⅱ)因为函数f(x)=x2-2x-3的对称轴为x=1.
若f(3)=f(2a-3),
则$\frac{3+2a-3}{2}$=1 或2a-3=3--------------------------(9分)
得 a=1或a=3.--------------------------(12分)
综上,a=1或a=3.
点评 本题考查二次函数的性质的应用,考查计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
12.在直三棱柱ABC-A1B1C1中,AC=AA1=2,∠ACB=90°,点E,F分别是棱AB,BB1的中点,当二面角C1-AA1-B为45°时,直线EF与BC1的夹角为( )
| A. | 60° | B. | 45° | C. | 90° | D. | 120° |
19.已知函数f(x)=kx-1,其中实数k随机选自区间[-1,2].则对任意的x∈[-1,1],f(x)≤0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
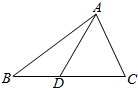 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.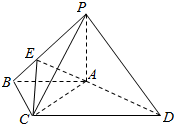 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.