题目内容
某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销.经试销发现:日销售量Q(件)与实际销售价x(元)满足关系:
Q=
(1)求总利润(利润=销售额-成本)y(元)与销售价x(件)的函数关系式;
(2)试问:当实际销售价为多少元时,总利润最大.
Q=
|
(1)求总利润(利润=销售额-成本)y(元)与销售价x(件)的函数关系式;
(2)试问:当实际销售价为多少元时,总利润最大.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)根据利润=销售额-成本,写出总利润y(元)与销售价x(件)的函数关系式;
(2)根据(1)中的函数关系式,在每一段上讨论函数的最大值,从而求出整个函数的最大值.
(2)根据(1)中的函数关系式,在每一段上讨论函数的最大值,从而求出整个函数的最大值.
解答:
解:(1)根据题意,得;
总利润y(元)与销售价x(件)的函数关系式是
y=
=
;
(2)由(1)得:
当5<x<7时,y=39(2x3-39x2+252x-535),
∴y′=234(x2-13x+42)=234(x-6)(x-7),
当5<x<6时,y′>0,y=f(x)为增函数,
当6<x<7时,y′<0,y=f(x)为减函数,
∴当x=6时,f(x)max=f(6)=195;
当7≤x<8时,y=6(33-x)∈(150,156];
当8≤x<13时,y=-10(x-9)2+160,
当x=9时,ymax=160;
综上知:当x=6时,总利润最大,最大值为195.
总利润y(元)与销售价x(件)的函数关系式是
y=
|
=
|
(2)由(1)得:
当5<x<7时,y=39(2x3-39x2+252x-535),
∴y′=234(x2-13x+42)=234(x-6)(x-7),
当5<x<6时,y′>0,y=f(x)为增函数,
当6<x<7时,y′<0,y=f(x)为减函数,
∴当x=6时,f(x)max=f(6)=195;
当7≤x<8时,y=6(33-x)∈(150,156];
当8≤x<13时,y=-10(x-9)2+160,
当x=9时,ymax=160;
综上知:当x=6时,总利润最大,最大值为195.
点评:本题考查了函数模型的应用问题,解题时列出函数解析式,从而分析函数的性质,是中档题目.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
以抛物线y=
x2的焦点为圆心,3为半径的圆与直线4x+3y+2=0相交所得的弦的长度是( )
| 1 |
| 4 |
A、
| ||||
B、4
| ||||
C、2
| ||||
| D、8 |
 若椭圆
若椭圆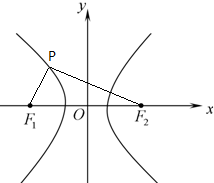 如图,若F1,F2是双曲线
如图,若F1,F2是双曲线