题目内容
已知函数f(x)=
,则函数F(x)=xf(x)-1的零点个数为( )
|
| A、7 | B、6 | C、5 | D、4 |
考点:函数的零点,分段函数的应用
专题:作图题,函数的性质及应用
分析:根据解析式函数f(x)=
,列出一部分解析式,画出f(x)与y=
图象,f(x)=
,解的个数,即可得出零点的个数.
|
| 1 |
| x |
| 1 |
| x |
解答:
 解:1-|x-1|=
解:1-|x-1|=
当3≤x<4,
f(x-2)=2-
,
当2≤x<3时,
f(x-2)=
(x-2)=
x-1
当4≤x<5时,
f(x-2)=
×[
(x-2)-1]=
×[
x-2]=
x-1,
当5≤x<6时,
f(x-2)=
×[2-
]=
×[3-
]=
-
当6≤x<7时,
f(x-2)=
×[
-1]=
-
,
当7≤x<8时,
f(x-2)=
×[
-
]=1-
,
f(x)=
f(x-2),向右平移2个单位,纵坐标缩短为
倍,
∵函数F(x)=xf(x)-1的零点,
∴f(x)=
,解的个数,
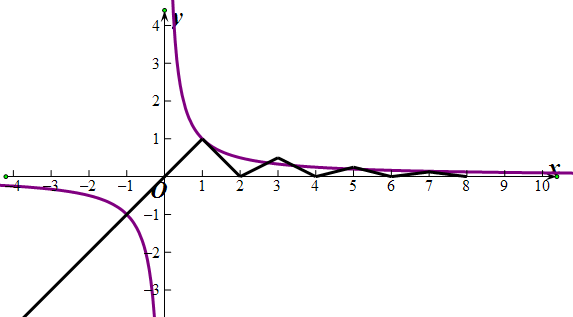
y=f(x),y=x交点个数
x=7时,f(7)=
,y=
,
<
从图象可知有6个交点,
所以函数F(x)=xf(x)-1的零点个数为6个,
故选:B
 解:1-|x-1|=
解:1-|x-1|=
|
当3≤x<4,
| 1 |
| 2 |
| x |
| 2 |
当2≤x<3时,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当4≤x<5时,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
当5≤x<6时,
| 1 |
| 2 |
| 1 |
| 2 |
| x-2 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 3 |
| 2 |
| x |
| 4 |
当6≤x<7时,
| 1 |
| 2 |
| 1 |
| 2 |
| x-2 |
| 4 |
| x |
| 8 |
| 3 |
| 4 |
当7≤x<8时,
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| x-2 |
| 4 |
| x |
| 8 |
f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∵函数F(x)=xf(x)-1的零点,
∴f(x)=
| 1 |
| x |
y=f(x),y=x交点个数
x=7时,f(7)=
| 1 |
| 8 |
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 7 |
所以函数F(x)=xf(x)-1的零点个数为6个,
故选:B
点评:本题考察了函数的图象,与函数的零点的关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=
,则f{f(-2)}的值为( )
|
| A、8 | B、9 | C、2 | D、3 |