题目内容
已知函数f(x)=
的最大值是M,最小值为N,则( )
| sinx+cosx+2x2+x |
| 2x2+cosx |
| A、M-N=4 |
| B、M+N=4 |
| C、M-N=2 |
| D、M+N=2 |
考点:三角函数的最值,同角三角函数基本关系的运用
专题:计算题,函数的性质及应用
分析:将f(x)=
转化为f(x)=
+1,构造函数g(x)=
,易知g(x)=
是奇函数,从而可得M+N=2.
| sinx+cosx+2x2+x |
| 2x2+cosx |
| sinx+x |
| 2x2+cosx |
| sinx+x |
| 2x2+cosx |
| sinx+x |
| 2x2+cosx |
解答:
解:∵f(x)=
=
+
=
+1,
令g(x)=
,
则g(-x)=
=
=-
=-g(x),
∴g(x)=
是奇函数,
∴g(x)的最大值与最小值之和为0,
∴f(x)的最大值与最小值之和为2,即M+N=2,
故选:D.
| sinx+cosx+2x2+x |
| 2x2+cosx |
=
| sinx+x |
| 2x2+cosx |
| cosx+2x2 |
| 2x2+cosx |
=
| sinx+x |
| 2x2+cosx |
令g(x)=
| sinx+x |
| 2x2+cosx |
则g(-x)=
| sin(-x)+(-x) |
| 2(-x)2+cos(-x) |
| -sinx-x |
| 2x2+cosx |
| sinx+x |
| 2x2+cosx |
∴g(x)=
| sinx+x |
| 2x2+cosx |
∴g(x)的最大值与最小值之和为0,
∴f(x)的最大值与最小值之和为2,即M+N=2,
故选:D.
点评:本题考查三角函数的最值,考查函数的奇偶性与最值,突出考查转化思想、创新思维与综合运算能力,属于难题.

练习册系列答案
相关题目
某三棱锥的三视图如图所示,该三棱锥的体积为( )


| A、2 | B、3 | C、4 | D、6 |
双曲线
-
=1(a>0,b>0)的离心率的取值范围正好是函数f(x)=2x+2-x(-1≤x≤2)的值域,则该双曲线渐近线的斜率取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||||||||||||
B、[
| ||||||||||||
C、[-
| ||||||||||||
D、[-
|
已知某几何体的三视图如图,则该几何体的体积是( )


| A、80 | ||||
B、64+
| ||||
| C、104 | ||||
D、80+8
|
如果球的大圆周长为C,则这个球的表面积是( )
A、
| ||
B、
| ||
C、
| ||
| D、2πC2 |
| 1 |
| 2 |
| 2 |
A、2
| ||
B、12
| ||
C、
| ||
| D、3 |
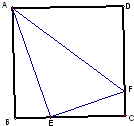 如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=
如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=